题目内容
【题目】知识再现
如图1,若点![]() ,
,![]() 在直线
在直线![]() 同侧,
同侧,![]() ,
,![]() 到
到![]() 的距离分别是3和2,
的距离分别是3和2,![]() ,现在直线
,现在直线![]() 上找一点
上找一点![]() ,使
,使![]() 的值最小,做法如下:
的值最小,做法如下:
作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,与直线
,与直线![]() 的交点就是所求的点
的交点就是所求的点![]() ,线段
,线段![]() 的长度即为
的长度即为![]() 的最小值,请你求出这个最小值.
的最小值,请你求出这个最小值.
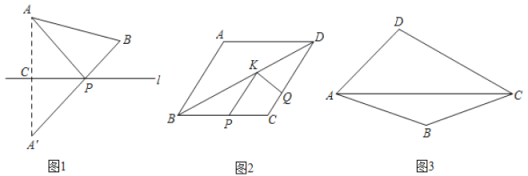
实践应用
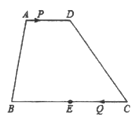
如图2,菱形![]() 中
中![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() ,
,![]() 上的任意一点,则
上的任意一点,则![]() 的最小值为______;
的最小值为______;
拓展延伸
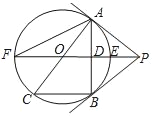
如图3,在四边形![]() 的对角线
的对角线![]() 上找一点
上找一点![]() ,使
,使![]() ,保留作图痕迹,不必写出作法.
,保留作图痕迹,不必写出作法.
【答案】知识再现:![]() ;
;
实践应用:![]()
拓展延伸:图形见详解
【解析】
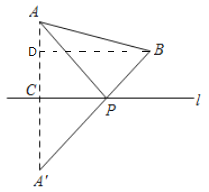
知识再现:根据对称性和勾股定理即可解题,
实践应用:先根据四边形ABCD是菱形可知,AD∥BC,由∠A=120°可知∠B=60°,作点P关于直线BD的对称点P′,连接P′Q,PC,则P′Q的长即为PK+QK的最小值,由图可知,当点Q与点C重合,CP′⊥AB时PK+QK的值最小,再在Rt△BCP′中利用锐角三角函数的定义求出P′C的长即可.
拓展延伸:作B关于AC的对称点,连接DE并延长,即可得出答案.
解:
知识再现:
由对称的性质得到![]()
∴AP+BP=![]()
过点B作BD⊥AC于D,
∴AC=3,CD=2,AD=1,![]()
在Rt△ADB中![]()
在Rt△![]() 中
中![]()
实践应用:∵四边形ABCD是菱形,
∴AD∥BC,
∵∠A=120°,
∴∠B=180°∠A=180°120°=60°,
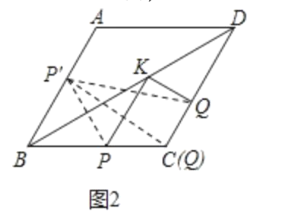
如图2中,作点P关于直线BD的对称点P′,连接P′Q,P′C,则P′Q的长即为PK+QK的最小值,由图可知,当点Q与点C重合,CP′⊥AB时PK+QK的值最小,
在Rt△BCP′中,
∵BC=AB=2,∠B=60°,
∴P′Q=CP′=BCsinB=2×![]() =
=![]()
故答案为![]()
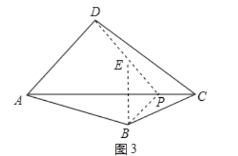
拓展延伸:如图3所示:作B关于AC的对称点E,连接DE并延长交AC于P即可.

练习册系列答案
相关题目