题目内容
【题目】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为![]() 千米,出租车离甲地的距离为
千米,出租车离甲地的距离为![]() 千米,两车行驶的时间为
千米,两车行驶的时间为![]() 小时,
小时,![]() 、
、![]() 关于
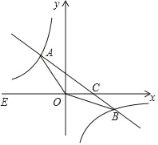
关于![]() 的函数图像如图所示:
的函数图像如图所示:
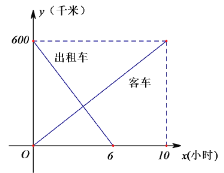
(1)根据图像,求出![]() 、
、![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)设两车之间的距离为![]() 千米.
千米.
①求两车相遇前![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②求出租车到达甲地后![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)甲、乙两地间有![]() 、
、![]() 两个加油站,相距200千米,若客车进入
两个加油站,相距200千米,若客车进入![]() 加油站时,出租车恰好进入
加油站时,出租车恰好进入![]() 加油站,求
加油站,求![]() 加油站离甲地的距离.
加油站离甲地的距离.
【答案】(1)y1=60x(0≤x≤10),y2=100x+600(0≤x≤6);(2)①S=y2y1=160x+600;②S=60x(6≤x≤10);(3)150km或300km.
【解析】
(1)直接运用待定系数法就可以求出y1、y2关于x的函数图关系式;
(2)①根据当0≤x<![]() 时,求出即可,②当6≤x≤10时,求出即可;
时,求出即可,②当6≤x≤10时,求出即可;
(3)分A加油站在甲地与B加油站之间,B加油站在甲地与A加油站之间两种情况列出方程求解即可.
解:(1)设y1=k1x,由图可知,函数图象经过点(10,600),
∴10k1=600,
解得:k1=60,
∴y1=60x(0≤x≤10),
设y2=k2x+b,由图可知,函数图象经过点(0,600),(6,0),则

解得:
![]()
∴y2=100x+600(0≤x≤6);
(2)①由题意,得
60x=100x+600
x=![]() ,即第
,即第![]() 小时两车相遇
小时两车相遇
当0≤x<![]() 时, S=y2y1=160x+600;
时, S=y2y1=160x+600;
②令y2=100x+600=0,解得:x=6
即第6小时出租车到达甲地
当6≤x≤10时,S=60x;
(3)由题意,得
①当A加油站在甲地与B加油站之间时,(100x+600)60x=200,
解得x=![]() ,
,
此时,A加油站距离甲地:60×![]() =150km,
=150km,
②当B加油站在甲地与A加油站之间时,60x(100x+600)=200,
解得x=5,此时,A加油站距离甲地:60×5=300km,
综上所述,A加油站到甲地距离为150km或300km.