题目内容
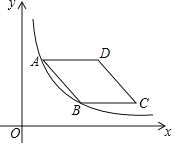
【题目】如图,点![]() ,
,![]() 分别是锐角
分别是锐角![]() 两边上的点,分别以点
两边上的点,分别以点![]() ,
,![]() 为圆心,以
为圆心,以![]() ,
,![]() 的长为半径画弧,两弧相交于点
的长为半径画弧,两弧相交于点![]() ,连接
,连接![]() ,
,![]() .
.

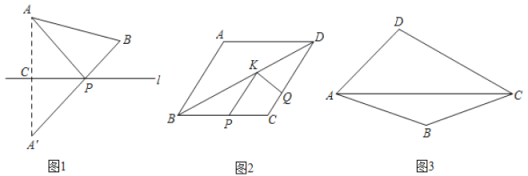
(1)请你判断所画四边形的形状,并说明理由;
(2)若![]() ,请判断此四边形的形状,并说明理由;
,请判断此四边形的形状,并说明理由;
(3)在(2)的条件下,连接![]() ,若
,若![]() 厘米,
厘米,![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)(2)见解析;(3)8![]() 厘米
厘米
【解析】
(1)根据题意得出ED=AF,AE=DF,进而利用平行四边形的判定解答即可;
(2)由AE=AF=ED=DF,根据四条边都相等的四边形是菱形,即可证得:四边形AEDF是菱形;
(3)首先连接EF,由AE=AF,∠A=60°,可证得△EAF是等边三角形,则可求得线段EF的长.
解:(1)四边形AEDF是平行四边形,
根据题意可得:ED=AF,AE=DF,
∴四边形AEDF是平行四边形;
(2)菱形.
理由:∵根据题意得:AE=AF=ED=DF,
∴四边形AEDF是菱形;
(3)连接EF,交AD于点O,

∵AE=AF,∠A=60°,
∴△EAF是等边三角形,
∴EF=AE=8厘米
∴EO=4,
由菱形的性质得∠AOE=90°,
在直角三角形AOE中,![]()
∴AD=2AO=8![]()

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目