题目内容
【题目】(1)问题发现,
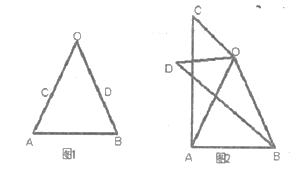
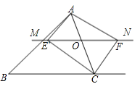
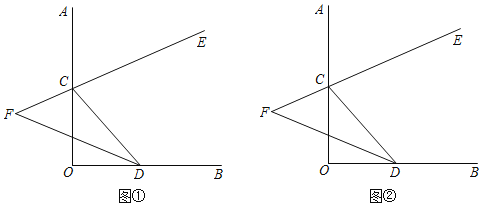
如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 上一点,将点
上一点,将点![]() 绕点
绕点![]() 顺时针旋转50°得到点
顺时针旋转50°得到点![]() ,则
,则![]() 与
与![]() 的数量关系是________________________。
的数量关系是________________________。
(2)类比探究
如图2,将(1)中的![]() 绕点
绕点![]() 在平面内旋转,(1)中的结论是否成立,并就图2的情形说明理由。
在平面内旋转,(1)中的结论是否成立,并就图2的情形说明理由。
(3)拓展延伸
![]() 绕点
绕点![]() 在平面旋转,当旋转到
在平面旋转,当旋转到![]() 时,请直接写出
时,请直接写出![]() 度数。
度数。
【答案】(1)![]() ;(2)成立,见解析;(3)115°或65°
;(2)成立,见解析;(3)115°或65°
【解析】
(1)根据旋转性质和等式性质可得;(2)根据旋转性质,证![]() 可得结论成立.(3)根据等腰三角形性质和平行线性质,分两种情况进行分析.
可得结论成立.(3)根据等腰三角形性质和平行线性质,分两种情况进行分析.
解:(1)根据旋转性质可得:OC=OD,因为OA=OB,
所以OA-OC=OB-OD
所以![]() ;
;
(2)成立
如图2,∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
(3)如图,当D在BO的左侧时
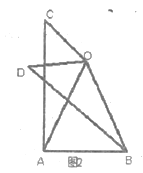
因为OA=OB
所以∠OAB=∠OBA=(180°-50°)÷2=65°
因为![]()
所以![]() =180°-∠OAB=180°-65°=115°
=180°-∠OAB=180°-65°=115°
同理,当D在MO的右侧时
![]() =∠OAB=65°
=∠OAB=65°
所以,![]() 的度数是:115°或65°.
的度数是:115°或65°.

练习册系列答案
相关题目
【题目】小明骑自行车去学校,最初以某一速度匀速行驶,中途自行车发生故障,停下来修车耽误了几分钟,为了按时到校,他加快了速度,仍保持匀速行驶,结果准时到校,到校后,小明画了自行车行进路程s(km)与行进时间t(h)的图象,如图所示,请回答:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:

时间t/h | 0 | 0.2 | 0.3 | 0.4 |
路程s/km |
(3)路程s可以看成时间t的函数吗?