题目内容
【题目】四边形ABCD是边长为4的正方形,点P是平面内一点.且满足BP⊥PC,现将点P绕点D顺时针旋转90度,则CQ的最大值=_____.

【答案】2+2![]() .
.
【解析】
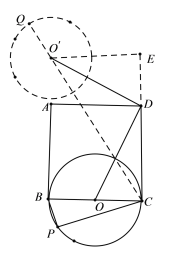
如图: 由BP⊥CP可知点P在以BC中点O为圆心,2为半径的圆上,⊙O绕点D旋转90°后为⊙O′,则P点旋转90°后的对应点Q在⊙O′上,所以CO′的延长线与⊙O′的交点是CQ的最大值,过O′作O′E⊥CD延长线于E,通过证明△DEO′≌△DOC可求出DE、EO′的长,根据勾股定理求出CO′的长,进而求出CQ的长即可.
如图:⊙O旋转90°得⊙O′,连接CO′交⊙O′于Q,则CQ即为所求,过O′作O′E⊥CD延长线于E,
∵BP⊥CP,
∴P点在在以BC中点O为圆心,2为半径的圆上,
∵⊙O′是⊙O旋转90°所得,
∴OD=O′D,
在△DEO′和△CDO中,∠DEO′=∠OCD=90°,∠DO′E=∠ODC,OD=O′D,
∴△DEO′≌△DOC,
∴DE=OC=2,EO′=CD=4,CE=6,
∴CO′=![]() =
=![]() ,
,
∴CQ=2+![]() .
.
故答案为:2+![]()

练习册系列答案
相关题目