题目内容
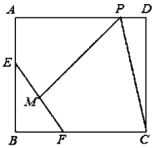
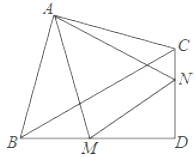
【题目】如图,在Rt△ABC和Rt△BCD中,∠BAC=∠BDC=90°,BC=4,AB=AC,∠CBD=30°,M,N分别在BD,CD上,∠MAN=45°,则△DMN的周长为_____.
【答案】2![]() +2
+2
【解析】
将△ACN绕点A逆时针旋转,得到△ABE,由旋转得出∠NAE=90°,AN=AE,∠ABE=∠ACD,∠EAB=∠CAN,求出∠EAM=∠MAN,根据SAS推出△AEM≌△ANM,根据全等得出MN=ME,求出MN=CN+BM,解直角三角形求出DC,即可求出△DMN的周长=BD+DC,代入求出答案即可.
将△ACN绕点A逆时针旋转,得到△ABE,如图:
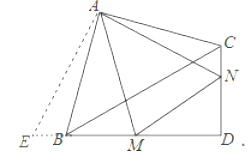
由旋转得:∠NAE=90°,AN=AE,∠ABE=∠ACD,∠EAB=∠CAN,
∵∠BAC=∠D=90°,
∴∠ABD+∠ACD=360°﹣90°﹣90°=180°,
∴∠ABD+∠ABE=180°,
∴E,B,M三点共线,
∵∠MAN=45°,∠BAC=90°,
∴∠EAM=∠EAB+∠BAM=∠CAN+∠BAM=∠BAC﹣∠MAN=90°﹣45°=45°,
∴∠EAM=∠MAN,
在△AEM和△ANM中,
 ,
,
∴△AEM≌△ANM(SAS),
∴MN=ME,
∴MN=CN+BM,
∵在Rt△BCD中,∠BDC=90°,∠CBD=30°,BC=4,
∴CD=![]() BC=2,BD=
BC=2,BD=![]() =2
=2![]() ,
,
∴△DMN的周长为DM+DN+MN=DM+DN+BM+CN=BD+DC=2![]() +2,
+2,
故答案为:2![]() +2.
+2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目