题目内容
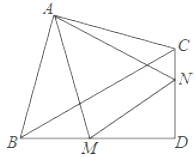
【题目】将一个矩形纸片OABC放置在平面直角坐标系xOy内,点A(6,0),点C(0,4),点O(0,0).点P是线段BC上的动点,将△OCP沿OP翻折得到△OC′P.
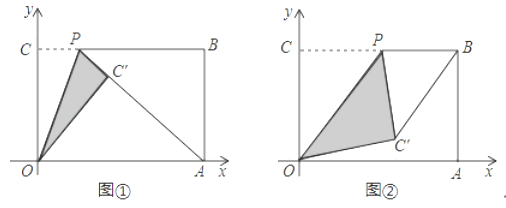
(Ⅰ)如图①,当点C′落在线段AP上时,求点P的坐标;
(Ⅱ)如图②,当点P为线段BC中点时,求线段BC′的长度.
【答案】(Ⅰ)P(6﹣2![]() ,4);(Ⅱ)BC′=
,4);(Ⅱ)BC′=![]()
【解析】
(Ⅰ)如图①,证明AO=AP=6,利用勾股定理求出PB即求出点P的坐标.
(Ⅱ)如图②,连接CC′交OP于D.解直角三角形求出PD,利用三角形的中位线定理即可解决问题.
(Ⅰ)∵A(5,0),点C(0,3),
∴OA=6,OC=4,
由翻折可知:∠OPC=∠OPA,
∵BC∥OA,
∴∠OPC=∠OPA,
∴∠POA=∠OPA,
∴OA=PA=6,
在Rt△PAB中,
∵∠B=90°,AB=4,PA=6,
∴PB=![]() =2
=2![]() ,
,
∴PC=BC﹣PB=6﹣2![]() ,
,
∴P(6﹣2![]() ,4).
,4).
(Ⅱ)如图②,连接CC′交OP于D.

在Rt△OPC中,∵OC=4,PC=3,
∴OP=![]() =5,
=5,
∵OP垂直平分线段CC′,
又∵![]() OPCD=
OPCD=![]() OCPC,
OCPC,
∴CD=![]() ,
,
PD=![]() ,
,
∵PC=PB,CD=DC′,
∴BC′=2PD=![]() .
.

练习册系列答案
相关题目