题目内容
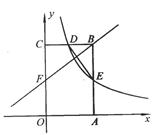
如图,矩形OABC的顶点A、C分别在x轴和y轴上,点 的坐标为(2,3).双曲线
的坐标为(2,3).双曲线 的图像经过BC的中点D,且与AB交于点E,连接DE.
的图像经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且ΔFCB∽ΔDBE,求直线FB的解析式
 的坐标为(2,3).双曲线
的坐标为(2,3).双曲线 的图像经过BC的中点D,且与AB交于点E,连接DE.
的图像经过BC的中点D,且与AB交于点E,连接DE.(1)求k的值及点E的坐标;
(2)若点F是边上一点,且ΔFCB∽ΔDBE,求直线FB的解析式

(1)3,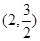 ;(2)
;(2)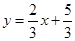 .
.
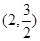 ;(2)
;(2)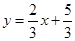 .
.试题分析:(1)首先根据点B的坐标和点D为BC的中点表示出点D的坐标,代入反比例函数的解析式求得k值,然后将点E的横坐标代入求得E点的纵坐标即可;
(2)根据△FBC∽△DEB,利用相似三角形对应边的比相等确定点F的坐标后即可求得直线FB的解析式.
(1)在矩形OABC中,
∵B点坐标为
 ,∴
,∴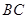 边中点
边中点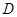 的坐标为(1,3)
的坐标为(1,3) 又∵双曲线
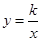 的图像经过点
的图像经过点 ∴
∴ ,
,∴
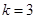
∵
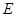 点在
点在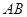 上,∴
上,∴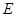 点的横坐标为2.
点的横坐标为2.又∵
 经过点
经过点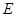 , ∴
, ∴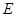 点纵坐标为
点纵坐标为 ,
,∴
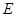 点纵坐标为
点纵坐标为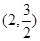
(2)由(1)得,
 ,
,∵△FBC∽△DEB,
∴
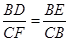 ,即
,即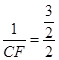 。
。∴
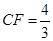 ,∴
,∴ ,即点
,即点 的坐标为
的坐标为
设直线
 的解析式为
的解析式为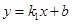 ,而直线
,而直线 经过
经过
∴
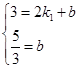 ,解得
,解得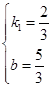
∴直线
 的解析式为
的解析式为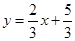

练习册系列答案
相关题目
 在第一象限内的图像与△ABC有交点,则
在第一象限内的图像与△ABC有交点,则 的取值范围是
的取值范围是


 轴、
轴、 轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,点D在双曲线
轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,点D在双曲线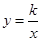 上,将正方形ABCD沿
上,将正方形ABCD沿 个单位长度后,点C恰好落在此双曲线上,则
个单位长度后,点C恰好落在此双曲线上,则 (x>0)的图象和矩形ABCD在第一象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,6).若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是 .
(x>0)的图象和矩形ABCD在第一象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,6).若将矩形向下平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是 .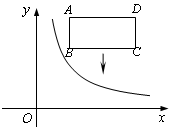
 在第一象限图象上的点,A1、A2、A3…An分别为x轴上的点,且△P1OA1、△P2A1A2、△P3A2A3…△PnAn-1An均为等边三角形.若点A1的坐标为(2,0),则点A2的坐标为__________________,点An的坐标为__________________.
在第一象限图象上的点,A1、A2、A3…An分别为x轴上的点,且△P1OA1、△P2A1A2、△P3A2A3…△PnAn-1An均为等边三角形.若点A1的坐标为(2,0),则点A2的坐标为__________________,点An的坐标为__________________.
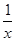 的图象上有三个点为(x1,y1)、(x2,y2)、(x3,y3),若y1<0<y2<y3,则x1,x2,x3的大小关系是 .
的图象上有三个点为(x1,y1)、(x2,y2)、(x3,y3),若y1<0<y2<y3,则x1,x2,x3的大小关系是 . 上的是( )
上的是( )
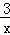 的图象上有两点A(x1,y1),B(x2,y2),若x1<0<x2,则下列判断正确的是()
的图象上有两点A(x1,y1),B(x2,y2),若x1<0<x2,则下列判断正确的是()