جâؤ؟ؤعبف
،¾جâؤ؟،؟شعز»جُض±دكةدزہ´خسذA،¢B،¢Cب¸ِ؛£µ؛£¬ؤ³؛£ر²´¬´سAµ؛³ِ·¢رطض±دكشبثظ¾B µ؛ت»دٍCµ؛£¬ض´ذذ؛£ر²بخخٌ£¬×îضص´ïµ½Cµ؛£®ةè¸أ؛£ر²´¬ذذت»x£¨h£©؛َ£¬سëB¸غµؤ¾àہëخھy£¨km£©£¬yسëxµؤ؛¯ت¹طدµبçح¼ثùت¾£® 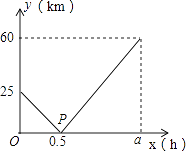
£¨1£©جî؟ص£؛A،¢Cء½¸غ؟ع¼نµؤ¾àہëخھkm£¬a=£»
£¨2£©اَyسëxµؤ؛¯ت¹طدµت½£¬²¢اë½âتحح¼ضذµمPµؤ×ّ±êثù±يت¾µؤتµ¼تزâزه£»
£¨3£©شعBµ؛سذز»²»¼ن¶د·¢ةنذإ؛إµؤذإ؛إ·¢ةنج¨£¬·¢ةنµؤذإ؛إ¸²¸ا°ë¾¶خھ15km£¬اَ¸أ؛£ر²´¬ؤـ½ستـµ½¸أذإ؛إµؤت±¼نسذ¶à³¤£؟
،¾´ً°¸،؟
£¨1£©85£»1.7h
£¨2£©½â£؛µ±0£¼x،ـ0.5ت±£¬ةèyسëxµؤ؛¯ت¹طدµت½خھ£؛y=kx+b£¬
،ك؛¯تح¼دٌ¾¹µم£¨0£¬25£©£¬£¨0.5£¬0£©£¬
،à ![]() £¬
£¬
½âµأ ![]() £®
£®
ثùزش£¬y=©پ50x+25£»
µ±0.5£¼x،ـ1.7ت±£¬ةèyسëxµؤ؛¯ت¹طدµت½خھ£؛y=mx+n£¬
،ك؛¯تح¼دٌ¾¹µم£¨0.5£¬0£©£¬£¨1.7£¬60£©£¬
،à ![]() £¬
£¬
½âµأ ![]() £®
£®
ثùزش£¬y=50x©پ25£»
£¨3£©½â£؛سة©پ50x+25=15£¬
½âµأx=0.2£¬
سة50x©پ25=15£¬
½âµأx=0.8£®
ثùزش£¬¸أ؛£ر²´¬ؤـ½ستـµ½¸أذإ؛إµؤت±¼نخھ£؛0.6h
،¾½âخِ،؟½â£؛£¨1£©سةح¼؟ةضھ£¬A،¢B¸غ؟ع¼نµؤ¾àہëخھ25£¬B،¢C¸غ؟ع¼نµؤ¾àہëخھ60£¬ ثùزش£¬A،¢C¸غ؟ع¼نµؤ¾àہëخھ£؛25+60=85km£¬
؛£ر²´¬µؤثظ¶بخھ£؛25،آ0.5=50km/h£¬
،àa=85،آ50=1.7h£®
ثùزش´ً°¸تا£؛85£¬1.7h£»

 ؟خجأب«½â×ض´ت¾ن¶خئھصآدµءذ´ً°¸
؟خجأب«½â×ض´ت¾ن¶خئھصآدµءذ´ً°¸ ²½²½¸ك؟عثمجâ؟¨دµءذ´ً°¸
²½²½¸ك؟عثمجâ؟¨دµءذ´ً°¸ µم¾¦ذآ½ج²ؤب«ؤـ½â¶ءدµءذ´ً°¸
µم¾¦ذآ½ج²ؤب«ؤـ½â¶ءدµءذ´ً°¸ ذ،ر§½ج²ؤحêب«½â¶ءدµءذ´ً°¸
ذ،ر§½ج²ؤحêب«½â¶ءدµءذ´ً°¸