题目内容
【题目】现有若干张如图1的正方形硬纸片A.B和长方形硬纸片C.
(1)小明利用这些硬纸片拼成了如图2的一个新正方形，用两种不同的方法，计算出了新正方形的面积，由此，他得到了一个等式：_____________
(2)小明再取其中的若干张(三种纸片都取到)拼成一个面积为a2+nab+2b2长方形，则n可取的正整数值为____，并请在图3位置画出拼成的图形。
(3)根据拼图的经验,请将多项式a2+4ab+3b2分解因式：
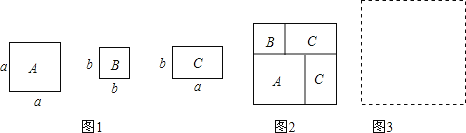
【答案】（1）a2+2ab+b2=(a+b)2；
（2）n=3,画图见解析；
（3）a2+4ab+3b2=(a+b)(a+3b)
【解析】（1）利用面积相等易得a2+2ab+b2=（a+b）2；（2）由于有a2+2b2，则a2+nab+2b2分解为（a+b）（a+2b），因此得到n=3，再画图；（3）利用面积可分解因式．
(1)a2+2ab+b2=(a+b)2；
(2)a2+nab+2b2=(a+b)(a+2b)，则n=3；
如图，
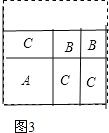
(3)a2+4ab+3b2=(a+b)(a+3b).
“点睛”本题考查了因式分解的应用：利用因式分解解决求值问题；利用因式分解解决证明问题；利用因式分解简化计算问题．
练习册系列答案
相关题目
