��Ŀ����
����Ŀ��������![]() ��
��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ��
��
��1��ֱ��д��������![]() �Ľ���ʽ��
�Ľ���ʽ��
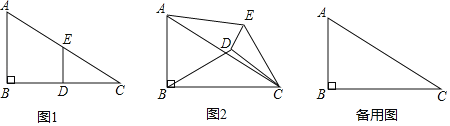
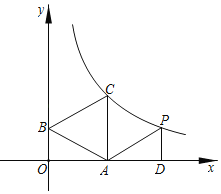
��2����ͼ1����![]() ��
��![]() ������������
������������![]() �ϣ�����
�ϣ�����![]() ������ƽ��4����λ���ȣ�������ƽ��
������ƽ��4����λ���ȣ�������ƽ��![]() ����λ���ȣ��õ��Ķ�Ӧ��
����λ���ȣ��õ��Ķ�Ӧ��![]() ǡ������������
ǡ������������![]() �ϣ���
�ϣ���![]() �����
�����![]() �����ꣻ
�����ꣻ
��3����ͼ2����������![]() ����ƽ��2����λ���ȵõ�������
����ƽ��2����λ���ȵõ�������![]() ��һ�κ���
��һ�κ���![]() ��ͼ��
��ͼ��![]() ��������
��������![]() ֻ��һ��������
ֻ��һ��������![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��̽����
��̽����![]() �����Ƿ���ڶ���
�����Ƿ���ڶ���![]() ����
����![]() �������ڣ������
�������ڣ������![]() �����ꣻ����˵�����ɣ�
�����ꣻ����˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3�����ڣ�
����3�����ڣ�![]()
��������
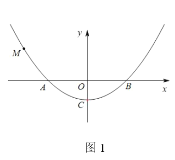
��1���������⣬�����B�����꣬Ȼ��B��C��������������ߵĽ���ʽ�м���������ۣ�
��2����![]() ����
����![]() �����ô���ϵ�������ֱ��MC�Ľ���ʽ������
�����ô���ϵ�������ֱ��MC�Ľ���ʽ������![]() ��
��![]() �ύ
�ύ![]() ��
��![]() �����ݵ�N��y���λ�ù�ϵ�������ۣ����á�Ǧ���ߣ�ˮƽ�����г����̣�����������ۣ�
�����ݵ�N��y���λ�ù�ϵ�������ۣ����á�Ǧ���ߣ�ˮƽ�����г����̣�����������ۣ�
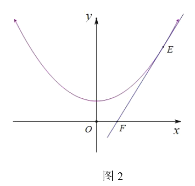
��3����������ɵ�ƽ�ƺ�Ķ��κ�������ʽΪ![]() ����
����![]() �����ֱ��l�Ľ���ʽ��Ȼ���������̣����=0�������
�����ֱ��l�Ľ���ʽ��Ȼ���������̣����=0�������![]() ������
������![]() ��
��![]() ��
��![]() ���Ƕ���
���Ƕ���![]() ������
������![]() ��
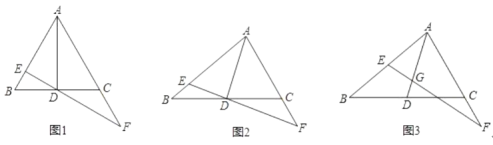
��![]() ���������������ε��ж�֤��
���������������ε��ж�֤��![]() ���г�����ʽ����������ۣ�
���г�����ʽ����������ۣ�
�⣺��1����![]()
��OC=1
��AB=4OC
��AB=4
�������ߵĶԳ���Ϊy��
��OB=2
���B��������2,0��
����B��C���������![]() ����
����
![]()
��������![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��2���⣺����![]() ����
����![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
����N��������룬��
�ɵã�![]() ��
��
����![]() ��
��![]() �ύ
�ύ![]() ��
��![]() ��
��
![]() ��
��
���һ������![]() ��
��![]() �����ʱ����
�����ʱ����![]()
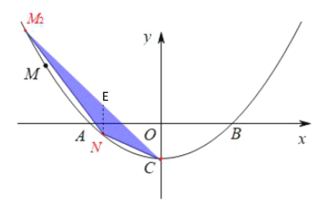
��![]()
![]()
��ã�![]() ��
��![]() ����ȥ����
����ȥ����
���ʱM![]()
�����������![]() ��
��![]() ���Ҳ�ʱ����
���Ҳ�ʱ����![]()
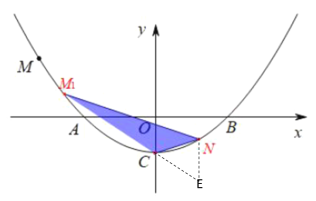
��![]()
![]()
��ã�![]()
���ʱ![]()
���ϣ�![]() ��
��![]() ��
��
��3���⣺���ڣ�
�������֪��ƽ�ƺ�Ķ��κ�������ʽΪ![]()
���������![]() ��
��
��![]() ����l��
����l��
�ɵ�![]() ��
��![]()
����
�����ã�![]()
![]()
![]()
��![]() ��
��![]()
��![]() ʱ����
ʱ����![]()
![]()
����![]() ��
��![]() ��
��![]() ���Ƕ���
���Ƕ���![]() ������
������![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
���HEG����EGH=90�㣬��OGF����EGH=90��
���HEG=��OGF
![]() ��
��
![]()
 ��
��
��ã�![]() ��
��![]() ����GΪ���㣬����ȥ��
����GΪ���㣬����ȥ��
![]() ��
��