题目内容
【题目】(1)如图1,直线AB∥CD,点P在两平行线之间,写出∠BAP、∠APC、∠DCP满足的数量关系.
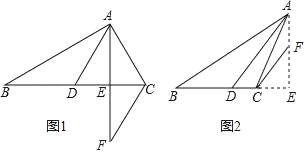
(2)如图2,直线AB与CD相交于点E,点P为∠AEC内一点,AQ平分∠EAP,CQ平分∠ECP,若∠AEC=40°,∠AQC=70°,求∠APC的度数.
(3)如图3,连接AD、CB交于点P,AQ平分∠BAD,CQ平分∠BCD,探究∠ABC、∠AQC、∠ADC满足的关系.

【答案】(1)∠BAP+∠DCP=∠APC;(2)100°;(3)∠ABC+∠ADC=2∠AQC.
【解析】
(1)过P作PE∥AB,利用平行线的性质:两直线平行内错角相等,易得到∠BAP、∠APC、∠DCP间关系;
(2)连接EQ并延长至G,连接QP并延长到H,利用角平分线的性质和三角形的外角等于不相邻的两个内角的关系,先得到∠QAP+∠QCP=30°,再得到∠APC的度数.
(3)利用角平分线的性质,得到∠BAQ=∠QAD,∠DCQ=∠QCB,利用三角形的外角等于不相邻的两个内角,通过∠BEQ、∠DFQ把∠ABC、∠AQC、∠ADC、连接起来得到结论.
解:(1)如图1所示,过P作PE∥AB,
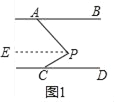
∵AB∥CD,∴PE∥CD
∵PE∥AB,∴∠BAP=∠APE,
同理,∠DCP=∠CPE
∴∠BAP+∠DCP=∠APE+∠CPE=∠APC
故答案为:∠BAP+∠DCP=∠APC,
(2)连接EQ并延长至G,

∵AQ平分∠EAP,CQ平分∠ECP,
∴∠EAQ=∠QAP,∠ECQ=∠QCP
∵∠AQG=∠QAE+∠AEQ,∠CQG=∠QCE+∠CEQ,
∴∠AQG+∠CQG=∠QAE+∠AEQ+∠QCE+∠CEQ,
即∠AQC=∠CEA+∠QAE+∠QCE
∵∠AEC=40°,∠AQC=70°
∴∠QAE+∠QCE=30°
即∠QAP+∠QCP=30°
连接QP并延长到H.
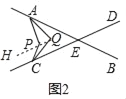
∵∠APH=∠AQP+∠PAQ,∠CPH=∠PQC+∠PCQ,
∴∠APH+∠CPH=∠AQP+∠PAQ+∠PQC+∠PCQ,
即∠APC=∠CQA+∠QAP+∠QCP
∴∠APC=30°+70°=100°.
(3)如图3中,

∵AQ平分∠BAD,CQ平分∠BCD,
∴∠BAQ=∠QAD,∠DCQ=∠QCB
∵∠BEQ=∠ABC+∠BAQ=∠BCQ+∠AQC,
∵∠QFD=∠ADC+∠QCD=∠QAD+∠AQC,
∴∠ABC+∠BAQ+∠ADC+∠QCD=∠BCQ+∠AQC+∠QAD+∠AQC
即∠ABC+∠ADC=2∠AQC.

【题目】为了解学生的体能情况,随机选取了1000名学生进行调查,并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
项目 | 长跑 | 短跑 | 跳绳 | 跳远 |
200 | √ | × | √ | √ |
300 | × | √ | × | √ |
150 | √ | √ | √ | × |
200 | √ | × | √ | × |
150 | √ | × | × | × |
(1)估计学生同时喜欢短跑和跳绳的概率;
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大?