Question

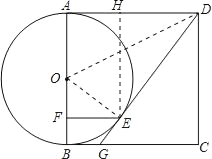
【题目】如图，以正方形ABCD的边AB为直径作⊙O，E是⊙O上的一点，EF⊥AB于F，AF＞BF，作直线DE交BC于点G．若正方形的边长为10，EF=4．

（1）分别求AF、BF的长．

（2）求证：DG是⊙O的切线．

Answer 1

【答案】（1）BF=2，AF=8（2）证明见解析

【解析】

（1）已知直径易知半径．连接OE，在Rt△OEF中运用勾股定理求OF，再求AF，BF；

（2）欲证DG为切线，则证OE⊥DG．连接OD，证明△OAD≌△OED即可．已有两边对应相等，只需证明DE＝AD．为此作EH⊥AD于H，运用勾股定理可证．

（1）连接OE，

∵正方形边长为10，AB是直径，

∴OB=OE=5．

∵EF⊥AB，EF=4，

∴OF==3，

∴BF=2，AF=8；

（2）连接OD，作EH⊥AD于H点．

∵四边形AFED为直角梯形，

∴EH=AF=8，HD=10﹣4=6．

∴DE==10．

∴AD=DE．

又OA=OE，OD公共边，

∴△OAD≌△OED，

∴∠OED=∠OAD=90°，

∴DG是⊙O的切线．