题目内容
【题目】直线MN与直线PQ垂直相交于点O，点A在射线OP上运动（点A不与点O重合），点B在射线OM上运动（点B不与点O重合）．
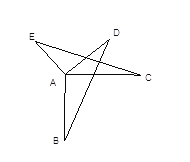
（1）如图1，已知AE、BE分别是∠BAO和∠ABO的角平分线，
①当∠ABO＝60°时，求∠AEB的度数；
②点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况：若不发生变化，试求出∠AEB的大小；
（2）如图2，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线所在的直线分别相交于E、F，在△AEF中，如果有一个角是另一个角的3倍，请直接写出∠ABO的度数．
【答案】（1）①135°②∠AEB的大小不会发生变化，∠AEB＝135°，详见解析（2）∠ABO＝60°
【解析】
（1）①根据三角形内角和定理、角分线定义，即可求解；
②方法同①，只是把度数转化为角表示出来，即可解答；
（2）根据三角形内角和定理及一个外角等于与它不相邻的两个内角和，利用角的和差计算即可求得结果，要对谁是谁的3倍分类讨论..
（1）如图1，①∵MN⊥PQ，
∴∠AOB＝90°，
∵∠ABO＝60°，
∴∠BAO＝30°，
∵AE、BE分别是∠BAO和∠ABO的角平分线，
∴∠ABE＝
∠ABO＝30°，∠BAE＝∠BAO＝15°，
∴∠AEB＝180°﹣∠ABE﹣∠BAE＝135°．
②∠AEB的大小不会发生变化．理由如下：
同①，得∠AEB＝180°﹣∠ABE﹣∠BAE＝180°﹣∠ABO﹣∠BAO
＝180°﹣（∠ABO+∠BAO）＝180°﹣×90°＝135°．
（2）∠ABO的度数为60°．理由如下：如图2，
∵∠BAO、∠OAG的角平分线与∠BOQ的角平分线所在的直线分别相交于E、F，∴∠OAE+∠OAF＝（∠BAO+∠GAO）＝90°，即∠EAF＝90°，
又∵∠BOA＝90°，
∴∠GAO＞90°，
①∵∠E＝
∠EAF＝30°，
∠EOQ＝45°，∠OAE+∠E＝∠EOQ＝45°，
∴∠OAE＝15°，
∠OAE＝∠BAO＝（90﹣∠ABO）
∴∠ABO＝60°．
②∵∠F＝3∠E，∠EAF=90°
∴∠E+∠F=90°
∴∠E=22.5°
∴∠EFA=90-22.5°=67.5°
∵∠EOQ＝∠EOM= ∠AOE= 45°，
∴∠BAO＝180°-(180°-45°-67.5°)×2=45°
∴∠ABO=90°-45°=45°
