题目内容
【题目】如图，正方形ABCD的边长为1，其面积标记为S1 ， 以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S2 ， …，按照此规律继续下去，则S2017的值为（ ） 
A.
B.
C.
D.
【答案】C
【解析】解：如图，∵正方形ABCD的边长为1，△CDE为等腰直角三角形，
∴DE2+CE2=CD2，DE=CE，
∴2S2=S1．
观察，发现规律：
S1=12=1，S2= 
S1= ，S3= S2= 
，S4= S3= 
，…，
∴Sn=（ ）n﹣1．
当n=2017时，S2017=（ ）2017﹣1=（ ）2016= 
，
故选：C．
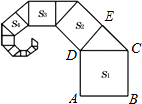
根据等腰直角三角形的性质可得出2S2=S1，写出部分Sn的值，根据数的变化找出变化规律Sn=（ ）n﹣1，依此规律即可得出结论．
练习册系列答案
相关题目
【题目】学校举行了主题为“让历史照亮未来”的演讲比赛，其中代表七、八年级参赛的两队各10人的比赛成绩如下表（10分制）：
七年级队 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
八年级队 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
（1）请直接写出七年级队成绩的中位数为 ， 八年级队成绩的众数为；
（2）若七、八年级队的平均成绩均为9分，请分别计算七、八年级队的方差．
