题目内容
【题目】如图,四边形ABCD中,∠BAD= 120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为 . 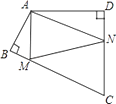
【答案】120°
【解析】作A关于BC和CD的对称点A′,A′′,交BC于M,交CD于N,根据轴对称的性质得出A′A′′即为△AMN周长的最小值.
∵∠BAD= 120°,
∴∠AA′A′′+∠AA′′A′=180°-120°=60°,
又∵A、A′关于BC对称,A、A′′关于CD对称,
∴∠MAA′=∠MA′A,∠NAA′′=∠NA′′A,
又∵∠AMN=∠MAA′+∠MA′A,∠ANM=∠NAA′′+∠NA′′A,
∴∠AMN+∠ANM=∠MAA′+∠MA′A+∠NAA′′+∠NA′′A,
=2(∠MA′A+∠NA′′A),
=2×60°,
=120°.
所以答案是:120°.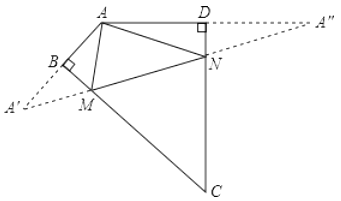
【考点精析】关于本题考查的三角形的外角和线段垂直平分线的性质,需要了解三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等才能得出正确答案.

练习册系列答案
相关题目