题目内容
【题目】阅读下列材料,并解爷其后的问题:
我们知道,三角形的中位线平行于第一边,且等于第三边的一半,我们还知道,三角形的三条中位线可以将三角形分成四个全等的一角形,如图1,若D、E、F分别是![]() 三边的中点,则有
三边的中点,则有![]() ,且
,且![]()



(1)在图1中,若![]() 的面积为15,则
的面积为15,则![]() 的面积为___________;
的面积为___________;
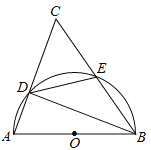
(2)在图2中,已知E、F、G、H分别是AB、BC、CD、AD的中点,求证:四边形EFGH是平行四边形;
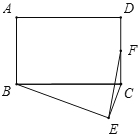
(3)如图3中,已知E、F、G、H分别是AB、BC、CD、AD的中点,![]() ,则四边形EFGH的面积为___________.
,则四边形EFGH的面积为___________.
【答案】(1)![]() ;(2)见解析;(3)5.
;(2)见解析;(3)5.
【解析】
(1)由三角形中位线定理得出DF∥BC,且DF=![]() BC,△ADF≌△DBE≌△FEC≌△EFD,得出△DEF的面积=
BC,△ADF≌△DBE≌△FEC≌△EFD,得出△DEF的面积=![]() △ABC的面积=
△ABC的面积=![]() 即可;
即可;
(2)连接BD,证出EH是△ABD的中位线,FG是△BCD的中位线,由三角形中位线定理得出EH∥BD,EH=![]() BD,FG∥BD,FG=
BD,FG∥BD,FG=![]() BD,得出EH∥FG,EH=FG,即可得出结论;
BD,得出EH∥FG,EH=FG,即可得出结论;
(3)证出EH是△ABD的中位线,FG是△BCD的中位线,由三角形中位线定理得出EH∥BD,EH=![]() BD=
BD=![]() ,FG∥BD,FG=
,FG∥BD,FG=![]() BD,得出EH∥FG,EH=FG,证出四边形EFGH是平行四边形,同理:EF∥AC,EF=
BD,得出EH∥FG,EH=FG,证出四边形EFGH是平行四边形,同理:EF∥AC,EF=![]() AC=2,证出EH⊥EF,得出四边形EFGH是矩形,即可得出结果.
AC=2,证出EH⊥EF,得出四边形EFGH是矩形,即可得出结果.
(1)解:∵D、E、F分别是△ABC三边的中点,
则有DF∥BC,且DF=![]() BC,△ADF≌△DBE≌△FEC≌△EFD,
BC,△ADF≌△DBE≌△FEC≌△EFD,
∴△DEF的面积=![]() △ABC的面积=
△ABC的面积=![]() ;
;
故答案为:![]() ;
;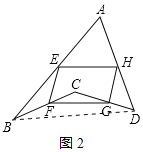
(2)证明:连接BD,如图2所示:
∵E、F、G、H分别是AB、BC、CD、AD的中点,
∴EH是△ABD的中位线,FG是△BCD的中位线,
∴EH∥BD,EH=![]() BD,FG∥BD,FG=
BD,FG∥BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
(3)解:∵E、F、G、H分别是AB、BC、CD、AD的中点,
∴EH是△ABD的中位线,FG是△BCD的中位线,
∴EH∥BD,EH=![]() BD=
BD=![]() ,FG∥BD,FG=
,FG∥BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形,
同理:EF∥AC,EF=![]() AC=2,
AC=2,
∵AC⊥BD,
∴EH⊥EF,
∴四边形EFGH是矩形,
∴四边形EFGH的面积=EH×EF=![]() ×2=5.
×2=5.
故答案为:(1)![]() ;(2)见解析;(3)5.
;(2)见解析;(3)5.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案