题目内容
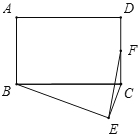
【题目】如图，在矩形ABCD中，AB＝6，AD＝8，以BC为斜边在矩形的外部作直角三角形BEC，点F是CD的中点，则EF的最大值为( )
A. 8B. 9C. 10D. 2
【答案】B
【解析】
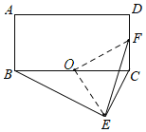
取BC中点O，连接OE，OF，根据矩形的性质可求OC，CF的长，根据勾股定理可求OF的长，根据直角三角形的性质可求OE的长，根据三角形三边关系可求得当点O，点E，点F共线时，EF有最大值，即EF=OE+OF．
解：如图，取BC中点O，连接OE，OF，
∵四边形ABCD是矩形，
∴AB=CD=6，AD=BC=8，∠C=90°，
∵点F是CD中点，点O是BC的中点，
∴CF=3，CO=4，
∴OF=
=5，
∵点O是Rt△BCE的斜边BC的中点，
∴OE=OC=4，
∵根据三角形三边关系可得：OE+OF≥EF，
∴当点O，点E，点F共线时，EF最大值为OE+OF=4+5=9．
故选：B．
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
