��Ŀ����
����Ŀ��ij�������������й���һ��![]() Ԫ��ǧ�˵���ɫʳƷ�������
Ԫ��ǧ�˵���ɫʳƷ�������![]() Ԫ��ǧ�����ۣ���ôÿ����۳�
Ԫ��ǧ�����ۣ���ôÿ����۳�![]() ǧ�ˣ������۾���֪��ÿ��������
ǧ�ˣ������۾���֪��ÿ��������![]() ��ǧ�ˣ������۵���
��ǧ�ˣ������۵���![]() ��Ԫ����
��Ԫ����![]() ����������ͼ��ʾ��һ�κ�����ϵ��
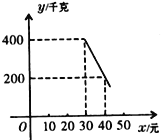
����������ͼ��ʾ��һ�κ�����ϵ��
��1�������y��x�ĺ�����ϵʽ��
��2�������������������۸���ɫʳƷÿ��������pԪ�������۵���Ϊ��ֵʱ��ÿ��ɻ�� ���������������Ƕ��٣�
��3�������г����飬����ɫʳƷÿ��ɻ�������4480Ԫ���ָó��о���Ҫ��ÿ�����õ���4180Ԫ����������ó���ȷ����ɫʳƷ���۵���x�ķ�Χ��ֱ��д����.
���𰸡���1��![]() ��30��x��50����
��30��x��50����
��2�������۵���Ϊ35Ԫ/ǧ��ʱ��ÿ��ɻ���������4500Ԫ��
��3��31��x��34��36��x��39��
��������������1����һ�κ�������ʽΪy=kx+b��Ȼ�����ͼ���ҳ�ֱ������������굱Ȼ���У��õ�����k��b�ķ����飬�ɴ˼�����⣻
��2������Ϊ�ɱ���20Ԫ/ǧ�ˣ�������Ϊy��ǧ�ˣ������۵���Ϊx����������=�����������ۼ�-�ɱ��ۣ�������⣻
��3�����ã�2���ĺ�������ʽ���ɵõ�����x��һԪ���η��̣��ⷽ�̼�����⣮
�����������1����![]() ��
��
��ͼ���֪��![]() ��
��
���![]()
��![]() ��
��
��2���������![]()
��a=-20��0����p�����ֵ��
��x=-1400/2��(-20)=35ʱ��p���ֵ=4500��
�������۵���Ϊ35Ԫ/ǧ��ʱ��ÿ��ɻ���������4500Ԫ��
��3����P=4420ʱ��4420=20x2+1400x20000��
���x1=33��x2=37��
��P=4180ʱ��4180=20x2+1400x20000��
��� x1=31��x2=39��
����ɫʳƷ���۵���Ϊ31x33��37x39�ķ�Χʱ����Ҫ��.