题目内容

【题目】如图所示，BC为⊙O的直径，弦AD⊥BC于E，∠C=60°． 求证：△ABD为等边三角形．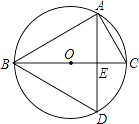

【答案】证明：∵BC为⊙O的直径，AD⊥BC， ∴AE=DE，
∴BD=BA，
∵∠D=∠C=60°，
∴△ABD为等边三角形．
【解析】根据垂径定理求出AE=DE，根据线段垂直平分线性质得出BA=BD，根据圆周角定理求出∠D=60°，根据等边三角形判定推出即可．
【考点精析】关于本题考查的等边三角形的判定和圆周角定理，需要了解三个角都相等的三角形是等边三角形；有一个角等于60°的等腰三角形是等边三角形；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案．

练习册系列答案
相关题目

【题目】我校全体同学参加了二年级刘XX同学的捐款活动，随机抽查了部分同学捐款的情况统计如图所示．

（1）本次共抽查学生　　　　　　人，并将条形图补充完整；

（2）捐款金额的众数是　　　　　　，平均数是　　　　　　；

（3）在我校2200名学生中，捐款15元及以上（含15元）的学生估计有多少人？

【题目】如图①，已知线段AC∥y轴，点B在第一象限，且AO平分∠BAC，AB交y轴于G，连接OB，OC.

(1)判断△AOG的形状，并予以证明；

(2)若点B，C关于y轴对称，求证：AO⊥BO；

(3)在(2)的条件下，如图②，点M为OA上一点，且∠ACM＝45°，BM交y轴于P，若点B的坐标为(3，1)，求点M的坐标．

【题目】把正整数1，2，3，4，…，2 009排列成如图所示的一个表．

(1)用一正方形在表中随意框住4个数，把其中最小的数记为x，另三个数用含x的式子表示出来，从小到大依次是__ __，__ __，__ __；

(2)在(1)前提下，当被框住的4个数之和等于416时，x的值是多少？

(3)在(1)前提下，被框住的4个数之和能否等于622？如果能，请求出此时x的值；如果不能，请说明理由．

【题目】设三角形三个内角的度数分别为x，y，z，如果其中一个角的度数是另一个角的度数的2倍，那么我们称数对(y，z)(y≤z)是x的和谐数对．例：当x＝150°时，对应的和谐数对有一个，它为(10，20)；当x＝66时，对应的和谐数对有二个，它们为(33，81)，(38，76)．当对应的和谐数对(y，z)有三个时，此时x的取值范围是____________．

【题目】如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连接AD、AG．

（1）求证：AD=AG；

（2）AD与AG的位置关系如何，请说明理由．

【题目】二次函数y=ax2+bx+c（a≠0）和正比例函数y= x的图象如图所示，则方程ax2+（b﹣ ）x+c=0（a≠0）的根的情况（ ）
A.两根都大于0
B.两根都等于0
C.两根都小于0
D.一根大于0，一根小于0

【题目】如图，大正方体上截去一个小正方体后，可得到图的几何体．

设原大正方体的表面积为，图中几何体的表面积为，那么与的大小关系是（ ）

、、、、不确定

小明说：“设图中大正方体各棱的长度之和为，图中几何体各棱的长度之和为，那么比正好多出大正方体条棱的长度．”若设大正方体的棱长为，小正方体的棱长为，请问为何值时，小明的说法才正确？

如果截去的小正方体的棱长为大正方体棱长的一半，那么图是图中几何体的表面展开图吗？如有错误，请在图中修正．

【题目】某车间有75名工人生产A、B两种零件，一名工人每天可生产A种零件15个或B 种 零件20个，已知1个B种零件需要配3个A种零件，该车间应如何分配工人，才能保证每天生产的两种零件恰好配套？设应安排x名工人生产A种零件，根据题意，列出的方程是___________________.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网