题目内容
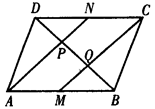
如图，□ABCD中，M、N分别是AB、CD的中点，BD分别交AN、CM于点 P、Q. 在结论： ①DP=PQ=QB ②AP=CQ ③CQ=2MQ ④S△ADP=
S□ABCD中，正确的个数为（ ）
A. 1 B. 2 C. 3 D. 4
S□ABCD中，正确的个数为（ ）A. 1 B. 2 C. 3 D. 4
C
平行四边形ABCD中，M、N分别是边AB、CD的中点，
∴DN=MB，∠MBC=∠NDA，AD=BC，∴△ADN≌△CBM，∴∠DNA=CMB，
∵AB∥CD，∴∠DNA=∠NAM，∴∠NAM=∠CMB，∴AN∥CM，
∵M是AB的中点，∴BQ=PQ，同理DP=PQ，因而DP=PQ=QB;
同理易证△APD≌△CBQ，则AP=CQ;
∵AB∥CD，∴△BMQ∽△DCQ，∴
=2，∴CQ=2MQ;
∵DP=PQ=QB，∴AN∥CM得到△ADP与平行四边形ABCD中AD边上的高的比是1：3，
∴S△ADP=
S平行四边形ABCD，∴正确结论的个数有3个．故选C．
∴DN=MB，∠MBC=∠NDA，AD=BC，∴△ADN≌△CBM，∴∠DNA=CMB，
∵AB∥CD，∴∠DNA=∠NAM，∴∠NAM=∠CMB，∴AN∥CM，
∵M是AB的中点，∴BQ=PQ，同理DP=PQ，因而DP=PQ=QB;
同理易证△APD≌△CBQ，则AP=CQ;
∵AB∥CD，∴△BMQ∽△DCQ，∴
=2，∴CQ=2MQ;∵DP=PQ=QB，∴AN∥CM得到△ADP与平行四边形ABCD中AD边上的高的比是1：3，
∴S△ADP=
S平行四边形ABCD，∴正确结论的个数有3个．故选C．
练习册系列答案
相关题目
