题目内容
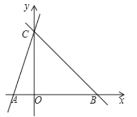
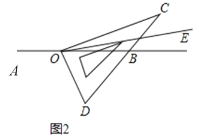
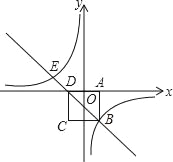
【题目】如图，在平面直角坐标系中，边长为2的正方形ABCD关于y轴对称，边AD在x轴上，点B在第四象限，直线BD与反比例函数
的图象交于点B、E．
（1）求反比例函数及直线BD的解析式；
（2）求点E的坐标．
【答案】（1）y=﹣
，y=﹣x﹣1；（2）E（﹣2，1）．
【解析】解：
(1)∵边长为2的正方形ABCD关于y轴对称，边AD在x轴上，点B在第四象限，
∴A(1，0)，D(－1，0)，B(1，－2)．
∵反比例函数
的图象过点B，
∴
，
解得m＝－2，
∴反比例函数的解析式为
．
设直线BD的解析式为y＝kx＋b，
∵y＝kx＋b的图象过B，D两点，
∴
解得
∴直线BD的解析式为y＝－x－1．
(2)∵直线BD与反比例函数
的图象交于点B，E，
∴
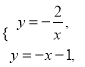
解得
或
∵B(1，－2)
∴E(－2，1)
练习册系列答案
相关题目
【题目】为了解某校初二学生每周上网的时间，两位学生进行了抽样调查．小丽调查了初二电脑爱好者中40名学生每周上网的时间；小杰从全校400名初二学生中随机抽取了40名学生，调查了每周上网的时间．小丽与小杰整理各自样本数据，如下表所示．
时间段（小时/周） | 小丽抽样（人数） | 小杰抽样（人数） |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
（1）你认为哪位学生抽取的样本不合理?请说明理由．
（2）专家建议每周上网2小时以上（含2小时）的学生应适当减少上网的时间，估计该校全体初二学生中有多少名学生应适当减少上网的时间.
