题目内容
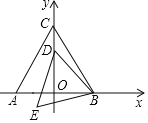
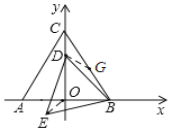
【题目】如图,△ABC是等边三角形,点A(-3,0),点B(3,0),点D是y轴上的一个动点,连接BD,将线段BD绕点B逆时针旋转60°,得到线段BE,连接DE,得到△BDE,则OE的最小值为______.
【答案】![]()
【解析】
取BC中点G,连接DG,由“SAS”可证△BGD≌△BOE,可得OE=DG,当DG⊥OC时,DG的值最小,由含30°角的直角三角形的性质即可求出DG的值,即OE最小值.
如图,取BC中点G,连接DG,OE,
∵△ABC是等边三角形,点A(-3,0),点B(3,0),
∴AO=BO=3,∠BCO=30°,∠ABC=60°,
∴BC=AB=6,
∵点G是BC中点,
∴CG=BG=OA=OB=3,
∵将线段BD绕点B逆时针旋转60°,
∴∠DBE=60°,BD=BE,
∴∠ABC=∠DBE,
∴∠CBD=∠ABE,且BE=BD,BG=OB=3,
∴△BGD≌△BOE(SAS),
∴OE=DG,
∴当DG⊥OC时,DG的值最小,即OE的值最小.
∵∠BCO=30°,DG⊥OC
∴DG=![]() CG=
CG=![]() ,
,
∴OE的最小值为![]() .
.
故答案为:![]()

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
【题目】为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示.
时间段(小时/周) | 小丽抽样(人数) | 小杰抽样(人数) |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(1)你认为哪位学生抽取的样本不合理?请说明理由.
(2)专家建议每周上网2小时以上(含2小时)的学生应适当减少上网的时间,估计该校全体初二学生中有多少名学生应适当减少上网的时间.