题目内容
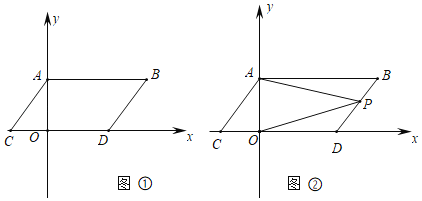
【题目】如图，在平面直角坐标系xOy中，A,B两点分别在x轴，y轴的正半轴上，且OA=OB，点C在第一象限，OC=3，连接BC，AC，若∠BCA=90°，则BC+AC的值为_________。
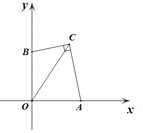
【答案】
【解析】
可将△OBC绕着O点顺时针旋转90°，所得的图形与△OAC正好拼成等腰直角三角形BC+AC等于等腰三角形的斜边CD.
解：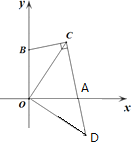
将△OBC绕O点旋转90°，
∵OB=OA
∴点B落在A处，点C落在D处
且有OD=OC=3，∠COD=90°，∠OAD=∠OBC，
在四边形OACB中
∵∠BOA=∠BCA=90°，
∴∠OBC+∠OAC=180°，
∴∠OAD+∠OAC=180°
∴C、A、D三点在同一条直线上，
∴△OCD为等要直角三角形，根据勾股定理
CD2=OC2+OD2
即CD2=32+32=18
解得CD=
即BC+AC=.
练习册系列答案
相关题目
【题目】张明、王成两位同学在初二学年10次数学单元检测的成绩（成绩均为整数，且个位数为0）如图所示利用图中提供的信息，解答下列问题：
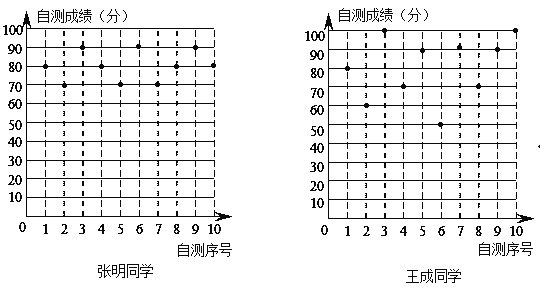
（1）完成下表：
姓名 | 平均成绩 | 中位数 | 众数 | 方差（s2） |
张明 |
| 80 | 80 |
|
王成 |
|
|
| 260 |
（2）如果将90分以上（含90分）的成绩视为优秀，则优秀率较高的同学是 ；
（3）根据图表信息，请你对这两位同学各提出学习建议．
