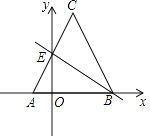题目内容
【题目】如图,已知直线y=3x﹣3分别交x轴,y轴于A,B两点,抛物线y=x2+bx+c经过A,B两点,点C是抛物线与x轴的另一个交点(与点A不重合),点D是抛物线的顶点,请解答下列问题. 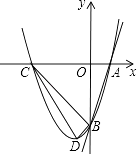
(1)求抛物线的解析式;
(2)判断△BCD的形状,并说明理由;
(3)求△BCD的面积.
【答案】
(1)解:∵直线y=3x﹣3分别交x轴,y轴于A,B两点,
当y=0时,x=1,当x=0时,y=﹣3,
∴点A(1,0),点B(0,﹣3),
∵抛物线y=x2+bx+c经过A,B两点,
∴ ![]() ,
,
解得, ![]() ,
,
∴抛物线的解析式为:y=x2+2x﹣3
(2)解:△BCD是直角三角形,
理由:∵y=x2+2x﹣3=(x+1)2﹣4=(x+3)(x﹣1),
∴当y=0时,x=﹣3或x=1,此抛物线的顶点坐标是(﹣1,﹣4),
∵抛物线y=x2+bx+c经过A,B两点,点C是抛物线与x轴的另一个交点(与点A不重合),点D是抛物线的顶点,
∴点C(﹣3,0),点D(﹣1,﹣4),
∵点B(0,﹣3),
∴BC= ![]() =3
=3 ![]() ,
,
CD= ![]() =2
=2 ![]() ,
,
BD= ![]() =
= ![]() ,
,
∵ ![]() ,
,
∴BC2+BD2=CD2,
∴△BCD是直角三角形
(3)解:由(2)知△BCD是直角三角形,∠CBD=90°, ![]() ,CD=2
,CD=2 ![]() ,BD=
,BD= ![]() ,
,
∴△BCD的面积是: ![]() ,
,
即△BCD的面积是3
【解析】(1)根据直线y=3x﹣3分别交x轴,y轴于A,B两点,可以求得点A和点B的坐标,由抛物线y=x2+bx+c经过A,B两点,从而可以得到抛物线的解析式;(2)根据(1)中的函数解析式可以分别求得点C和点D的坐标,从而可以求得BC、BD、CD的长,然后根据勾股定理的逆定理即可解答本题;(3)根据(2)中的判断,然后根据三角形的面积公式即可解答本题.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.

 名校课堂系列答案
名校课堂系列答案