��Ŀ����
����Ŀ������ƽ��ֱ���ϸ���![]() ���㣬����
���㣬����![]() ���㰴���¹��������߶Σ�
���㰴���¹��������߶Σ�
��ƽ����֮��ĵ������߶�ʱ�������й�ͬ�Ķ˵㣬���������������㣻
�ڷ��Ϣ�Ҫ����߶α���ȫ��������
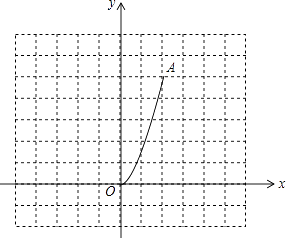
ͼ![]() չʾ�˵�
չʾ�˵�![]() ʱ���������ʱͼ�������εĸ���Ϊ
ʱ���������ʱͼ�������εĸ���Ϊ![]() ��ͼ
��ͼ![]() չʾ�˵�
չʾ�˵�![]() ʱ��һ���������ʱͼ�������εĸ���Ϊ
ʱ��һ���������ʱͼ�������εĸ���Ϊ![]() ���Իش��������⣺
���Իش��������⣺
![]() ��
��![]() ʱ������ͼ
ʱ������ͼ![]() �л���ʹ�����θ������ٵ�ͼ�Σ���ʱͼ�������εĸ�����________��
�л���ʹ�����θ������ٵ�ͼ�Σ���ʱͼ�������εĸ�����________��
![]() �Բ��뵱��
�Բ��뵱��![]() �Ե�ʱ��������������ͼ���У�������________�������Σ�
�Ե�ʱ��������������ͼ���У�������________�������Σ�
![]() ��
��![]() ʱ��������������ͼ���У�������________�������Σ�
ʱ��������������ͼ���У�������________�������Σ�
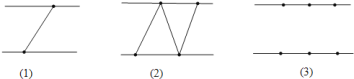
���𰸡�42��n-1��4022
��������
��1���������⻭��ͼ�Σ�����ͼ�����������θ������ɵó��𰸣�
��2�������ɵã���n��1ʱ���������ʱͼ�������εĸ���Ϊ0����0��2��11������n��2ʱ��һ���������ʱͼ�������εĸ���Ϊ2����2��2��21�������ʵ���n�Ե�ʱ�����ٿ��Ի�2��n1���������Σ�
��3����n��2012ʱ��������������ͼ���У�������2����20121����4022�������Σ�
��1��
��ͼ��
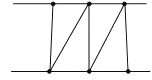
��ʱͼ�������εĸ����ǣ�4����
�ʴ�Ϊ��4��
��2������n�Ե�ʱ�����ٿ��Ի�2��n1���������Σ�
�ʴ�Ϊ��2��n1����
��3��2����20121����4022����
��n��2012ʱ�����ٿ��Ի�4022����������
�ʴ�Ϊ��4022��

 ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ͬ����ϰ����ʦ����ѧ������ϵ�д�
ͬ����ϰ����ʦ����ѧ������ϵ�д�