题目内容
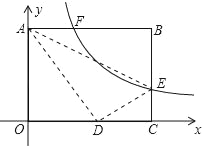
【题目】如图，在平面直角坐标系中，点A在第一象限，⊙A与x轴交于B（2，0）、C（8，0）两点，与y轴相切于点D，则点A的坐标是（ ）
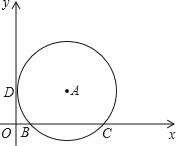
A. （5，4） B. （4，5） C. （5，3） D. （3，5）
【答案】A
【解析】
因为点A在第一象限，⊙A与x轴交于B（2，0）、C（8，0）两点，与y轴相切于点D，所以OB=2，OC=8，BC=6，连接AD，则AD⊥OD，过点A作AE⊥OC于E，则ODAE是矩形，由垂径定理可知BE=EC=3，所以OE=AD=5，再连接AB，则AB=AD=5，利用勾股定理可求出AE=4，从而就求出了A的坐标．
连接AD，AB，AC，再过点A作AE⊥OC于E，
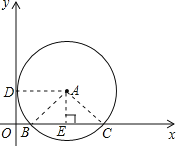
则ODAE是矩形，
∵点A在第一象限，⊙A与x轴交于B（2，0）、C（8，0）两点，与y轴相切于点D，
∴OB=2，OC=8，BC=6，
∵⊙A与y轴相切于点D，
∴AD⊥OD，
∵由垂径定理可知：BE=EC=3，
∴OE=AD=5，
∴AB=AD=5，
利用勾股定理知AE=4，
∴A（5，4）．
故选：A．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
【题目】王老师将
个黑球和若干个白球放入一个不透明的口袋并搅匀，让若干学生进行摸球实验，每次摸出一个球（有放回），下表是活动进行中的一组统计数据．
摸球的次数 |
|
|
|
|
|
|
摸到黑球的次数 |
|
|
|
|
|
|
摸到黑球的频率 |
|
|
|
|
|
补全上表中的有关数据，根据上表数据估计从袋中摸出一个球是黑球的概率是________（精确到0.01）；
估算袋中白球的个数；
在的条件下，若小强同学有放回地连续两次摸球，用画树状图或列表的方法计算他两次都摸出白球的概率．
