题目内容
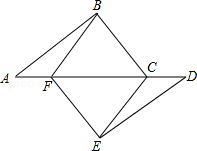
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.
(1)证明:∠BAC=∠DAC.
(2)若∠BEC=∠ABE,试证明四边形ABCD是菱形.

【答案】证明见解析
【解析】
试题由AB=AD,CB=CD结合AC=AC可得△ABC≌△ADC,由此可得∠BAC=∠DAC,再证△ABF≌△ADF即可得到∠AFB=∠AFD,结合∠AFB=∠CFE即可得到∠AFD=∠CFE;
(2)由AB∥CD可得∠DCA=∠BAC结合∠BAC=∠DAC可得∠DCA=∠DAC,由此可得AD=CD结合AB=AD,CB=CD可得AB=BC=CD=AD,即可得到四边形ABCD是菱形.
试题解析:
(1)在△ABC和△ADC中,
∵AB=AD,CB=CD,AC=AC,
∴△ABC≌△ADC,
∴∠BAC=∠DAC,
在△ABF和△ADF中,
∵AB=AD,∠BAC=∠DAC,AF=AF,
∴△ABF≌△ADF,
∴∠AFB=∠AFD.
(2)证明:∵AB∥CD,
∴∠BAC=∠ACD,
∵∠BAC=∠DAC,
∴∠ACD=∠CAD,
∴AD=CD,
∵AB=AD,CB=CD,
∴AB=CB=CD=AD,
∴四边形ABCD是菱形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目