题目内容
【题目】如图,D为等边三角形ABC内的一点,DA=5,DB=4,DC=3,将线段AD以点A为旋转中心逆时针旋转60°得到线段AD′,下列结论:①点D与点D′的距离为5;②∠ADC=150°;③△ACD′可以由△ABD绕点A逆时针旋转60°得到;④点D到CD′的距离为3;⑤S四边形ADCD′ =6+![]() .其中正确的有( )
.其中正确的有( )

A.2个B.3个C.4个D.5个
【答案】B
【解析】
连结DD′,根据旋转的性质得AD=AD′,∠DAD′=60°,可判断△ADD′为等边三角形,则DD′=5,可对①进行判断;由△ABC为等边三角形得到AB=AC,∠BAC=60°,则把△ABD逆时针旋转60°后,AB与AC重合,AD与AD′重合,于是可对③进行判断;再根据勾股定理的逆定理得到△DD′C为直角三角形,则可对②④进行判断;由于四边形ADCD′的面积=△ADD′的面积+△D′DC的面积,利用等边三角形的面积公式和直角三角形面积公式计算后可对⑤进行判断.
解:连结DD′,如图,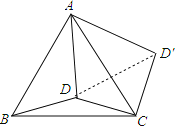
∵线段AD以点A为旋转中心逆时针旋转60°得到线段AD′,
∴AD=AD′,∠DAD′=60°,
∴△ADD′为等边三角形,
∴DD′=5,所以①正确;
∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∴把△ABD逆时针旋转60°后,AB与AC重合,AD与AD′重合,
∴△ACD′可以由△ABD绕点A逆时针旋转60°得到,所以③正确;
∴D′C=DB=4,
∵DC=3,
在△DD′C中,
∵32+42=52,
∴DC2+D′C2=DD′2,
∴△DD′C为直角三角形,
∴∠DCD′=90°,
∵△ADD′为等边三角形,
∴∠ADD′=60°,
∴∠ADC≠150°,所以②错误;
∵∠DCD′=90°,
∴DC⊥CD′,
∴点D到CD′的距离为3,所以④正确;
∵S△ADD′+S△D′DC
![]()
=6+![]() 所以⑤错误.
所以⑤错误.
故选:B.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案




