题目内容
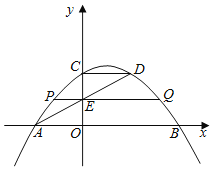
【题目】如图，抛物线
与x轴相交于
两点，与
轴相交于点
，点
在抛物线上，且
．
与轴相交于点
，过点的直线
平行于
轴，与拋物线相交于
两点，则线段的长为_____．
【答案】
【解析】
利用二次函数图象上点的坐标特征可求出点A，B，C，D的坐标，由点A，D的坐标，利用待定系数法可求出直线AD的解析式，利用一次函数图象上点的坐标特征可求出点E的坐标，再利用二次函数图象上点的坐标特征可得出点P，Q的坐标，进而可求出线段PQ的长．
解：由图可知，
当
时，
，
解得：
，
，
∴点
的坐标为
；
当
时，
，
∴点
的坐标为(0，2)；
当
时，
，
解得：
，
，
∴点
的坐标为
．
设直线
的解析式为
，
将
，
代入
，得：
，解得：
，
∴直线的解析式为
．
当时，
，
∴点
的坐标为
．
当
时，
，
解得：
，
，
∴点
的坐标为
，点
的坐标为
，
∴
．
故答案为：．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
