题目内容
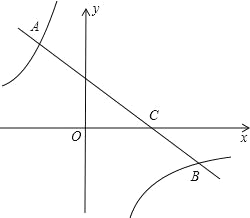
【题目】如图，一次函数 y=kx+2（k＜0）的图象经过点 C（3，0），且反比例函数 y=
的图象与该一次函数的图象交于第二、四象限内的 A，B 两点．
(1)求该一次函数的解析式；
(2)若 AC=2BC，求 m 的值．
【答案】（1）y=﹣
x+2；（2）﹣12．
【解析】
（1）依据一次函数 y=kx+2（k＜0）的图象经过点 C（3，0），可得 k=﹣，进而得到一次函数的解析式；
（2）作 AD⊥x 轴于点 D，BE ⊥x 轴于点 E，依据△ACD∽△BCE，可得 AD=2BE．设B 点纵坐标为﹣n，则 A 点纵坐标为 2n，进而得到 A（3﹣3n，2n），B（3+
n，﹣n），依据反比例函数 y=
的图象经过 A、B 两点，即可得到 m 的值．
解：（1）∵一次函数 y =kx+2（k＜0）的图象经过点 C（3，0），
∴3k+2=0， 解得 k=﹣，
∴一次函数的解析式为 y=﹣ x+2；
（2）如图，作 AD⊥x 轴于点 D，BE⊥x 轴于点 E，则 AD∥BE．
∵AD∥BE，
∴△ACD∽△BCE，
∴
=2，
∴ AD=2BE．
设 B 点纵坐标为﹣n，则 A 点纵坐标为 2n．
∵直线 AB 的解析式为 y=﹣x+2，
∴A（3﹣3n，2n），B（3+n，﹣n），
∵反比例函数 y=的图象经过 A、B 两点，
∴（3﹣3n）2n=（3+n）（﹣n），解得 n1=2，n2=0（不合题意，舍去），
∴m=（3﹣3n）2n=﹣3×4=﹣12．
阅读快车系列答案
【题目】小华是花店的一名花艺师，她每天都要为花店制作普通花束和精致花束，她每月工作20天，每天工作8小时，她的工资由基本工资和提成工资两部分构成，每月的基本工资为l800元，另每制作一束普通花束可提2元，每制作一束精致花束可提5元．她制作两种花束的数量与所用时间的关系见下表：
制作普通花束（束） | 制作精致花束（束） | 所用时间（分钟） |
10 | 25 | 600 |
15 | 30 | 750 |
请根据以上信息，解答下列问题：
（1）小华每制作一束普通花束和每制作一束精致花束分别需要多少分钟？
（2）2019年11月花店老板要求小华本月制作普通花束的总时间
不少于3000分钟且不超过5000分钟，则小华该月收入
最多是多少元？此时小华本月制作普通花束和制作精致花束分别是多少束？
