题目内容
【题目】阅读下面的材料,然后解答问题:
我们新定义一种三角形,两边的平方和等于第三边平方的k倍的三角形叫做“k倍三角形”(k为正实数).
(1)理解:根据“k倍三角形”的定义填空(填“锐角”、“直角”或“钝角”):
①当![]() 时,k倍三角形一定是_____________三角形;
时,k倍三角形一定是_____________三角形;
②当![]() 时,k倍三角形一定是______________三角形.
时,k倍三角形一定是______________三角形.
(2)探究:当![]() 时,已知Rt△ABC为“k倍三角形”,且
时,已知Rt△ABC为“k倍三角形”,且![]() ,
,![]() ,求所有满足条件的k值.
,求所有满足条件的k值.
(3)拓展:若Rt△ABC是“k倍三角形”,且![]() ,
,![]() ,
,![]() ,
,![]() .当
.当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)①直角;②钝角;(2)3或2或5;(3)![]() 或
或![]() .
.
【解析】
(1)设三角形三边分别为a、b、c,
①当![]() 时,可以得到
时,可以得到![]() ,三边满足勾股定理即可判断三角形为直角三角形;
,三边满足勾股定理即可判断三角形为直角三角形;
②当![]() 时,可以得到
时,可以得到![]() ,可以判断三角形为钝角三角形;
,可以判断三角形为钝角三角形;
(2)当![]() 时,Rt△ABC为“k倍三角形”,由
时,Rt△ABC为“k倍三角形”,由![]() ,
,![]() ,利用勾股定理求出第三边,需要分情况讨论:当AB是斜边时;当AB是直角边时两种情况求解即可 ;
,利用勾股定理求出第三边,需要分情况讨论:当AB是斜边时;当AB是直角边时两种情况求解即可 ;
(3)若Rt△ABC是“k倍三角形”,根据题意可得三边关系式,结合勾股定理得到方程组,求解即可表示![]() 的值.
的值.
(1)设三角形三边分别为a、b、c,
①当![]() 时,可以得到
时,可以得到![]() ,则三角形是直角三角形,
,则三角形是直角三角形,
故答案为:直角;
②当![]() 时,可以得到
时,可以得到![]() ,则三角形为钝角三角形,
,则三角形为钝角三角形,
故答案为:钝角;
(2)当![]() 时,已知Rt△ABC为“k倍三角形”,且
时,已知Rt△ABC为“k倍三角形”,且![]() ,
,![]() ,分以下情况:
,分以下情况:
①当AB为斜边时,由![]() ,
,
∴![]() ,解得AC=
,解得AC=![]() ,
,
由![]() ,
,
可得:4+2=2k,
解得:k=3;
②当AB为直角边时,由![]() ,
,
∴![]() ,解得AC=
,解得AC=![]() ,
,
由![]() 或者
或者![]() ,
,
可得:6+2=4k,或者4+6=2k,
解得:k=2或者k=5,
综上所述,满足条件的k值为3或2或5;
故答案为:3或2或5;
(3)在Rt△ABC中,![]() ,
,
又∵k=2,
∴![]() 或
或![]() ,
,
∴联立方程组得
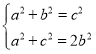 或
或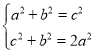 ,
,
解得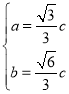 或
或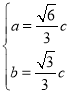 ,
,
∴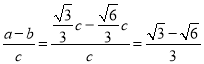 或
或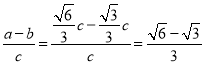 ,
,
∴![]() 的值为:
的值为:![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() .
.