题目内容
 已知:如图,在四边形ABCD中,∠ABC=90°,DE⊥AC于点F,交AB的延长线于点E,且AE=AC.(1)试说明:△ABF是等腰三角形;
已知:如图,在四边形ABCD中,∠ABC=90°,DE⊥AC于点F,交AB的延长线于点E,且AE=AC.(1)试说明:△ABF是等腰三角形;(2)若AD=DC,试说明:AC=2AB.
分析:(1)根据AAS证出△ABC≌△AFE,根据全等三角形的性质推出即可;
(2)因为AC⊥DE,若AD=DC,则可证明DE是AC的垂直平分线,即F是AC的中点,因为三角形ABC是直角三角形,再利用直角三角形斜边上的中线等于斜边的一半即可证明.
(2)因为AC⊥DE,若AD=DC,则可证明DE是AC的垂直平分线,即F是AC的中点,因为三角形ABC是直角三角形,再利用直角三角形斜边上的中线等于斜边的一半即可证明.
解答:(1)证明:∵∠ABC=90°,DE⊥AC,
∴∠ABC=∠AFE=90°,
在△ABC和△AFE中
∵
,
∴△ABC≌△AFE(AAS),
∴AB=AF,
∴△ABF是等腰三角形;
(2)∵DE⊥AC于点F,AD=DC,
∴DE是AC的垂直平分线,
∴F是AC的中点,
∵∠ABC=90°,
∴△ABC是直角三角形,
∴BF=
AC,
∵AB=AF,
∴AC=2AB
∴∠ABC=∠AFE=90°,
在△ABC和△AFE中
∵
|
∴△ABC≌△AFE(AAS),
∴AB=AF,
∴△ABF是等腰三角形;
(2)∵DE⊥AC于点F,AD=DC,
∴DE是AC的垂直平分线,
∴F是AC的中点,
∵∠ABC=90°,
∴△ABC是直角三角形,
∴BF=
| 1 |
| 2 |
∵AB=AF,
∴AC=2AB
点评:本题考查了全等三角形的判定和性质、等腰三角形的判定和性质以及直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
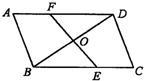 39、已知:如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O.求证:O是BD的中点.
39、已知:如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O.求证:O是BD的中点.
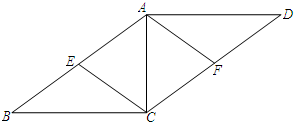 已知:如图,在四边形ABCD中,AD∥BC,AC⊥BC,点E、F分别是边AB、CD的中点,AF=CE.求证:AD=BC.
已知:如图,在四边形ABCD中,AD∥BC,AC⊥BC,点E、F分别是边AB、CD的中点,AF=CE.求证:AD=BC.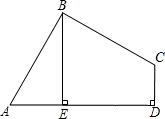 已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2. 已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.
已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.