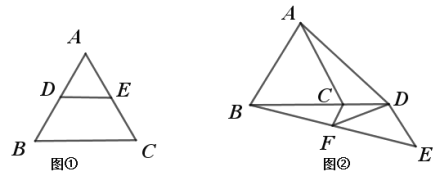��Ŀ����
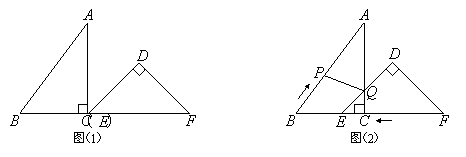
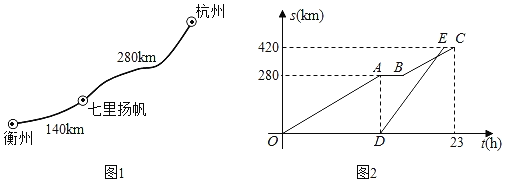
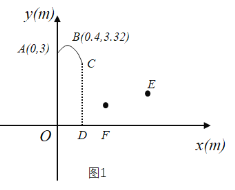
����Ŀ������������У�����Ͷ�������ڵ�A�����������������˶���·��Ϊ�����ߵ�һ���֣���ͼ1��ʾ����ֱ������ϵ���������߶���Ϊ��B��
��1����������ߵĺ�������ʽ��
��2�������˶�����Cʱ������������CD��x���ڵ�D��CD��2.6m��
����OD�ij���
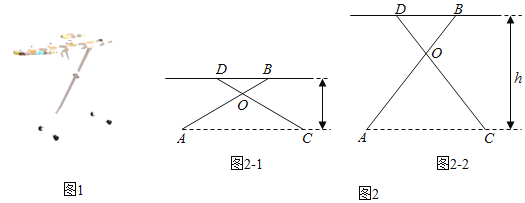
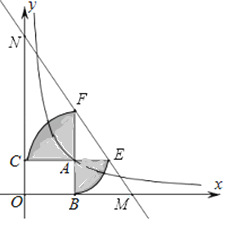
�ڶ��������������Է�������Ͷ�������ڵ�D����ֱ���������뽫����ֱ�߿��ٴ������ѻ�����Ŀ��Ϊ�����Ľ����E��4��1.3�������������������������߶�h1��m��������ǰ���붫��������ʱ��t��s�����㺯����ϵʽh1����2��t��0.5��2+2.7��0��t��1����С���ڵ�F��1.5��0�������أ����ȶ�����0.3s��ֱ�����������ظ߶�h2��m���붫��������ʱ��t��s���ĺ�����ϵ��ͼ2��ʾ���������������ߵ���״��ͬ����������ֱ�ߴ����ܷ�Խ��С�������ش�����E�����ܣ�����Ӧ��������ʲôʱ�䷶Χ�ڴ��������ܣ���˵�����ɣ�ֱ�ߴ�����������˶�ʱ����Բ��ƣ���

���𰸡���1��y����2��x��0.4��2+3.32����2����1m�����ܣ�![]()
��������
��1����y��a��x��0.4��2+3.32��a��0������A��0��3��������⼴�ɵó��𰸣�
��2���ٰ�y��2.6����y����2��x��0.4��2+3.32���ⷽ�����x�����ɵó�OD��1m��
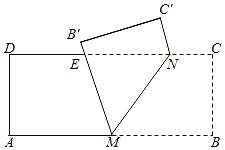
�ڶ����ڵ�D��������С���ڵ�F�����ص�ʾ��ͼ��ͼ2����MD��h1��NF��h2������M��N��E���㹲��ʱ������E��EG��MD�ڵ�G����NF�ڵ�H������N��NP��MD�ڵ�P��֤����MPN�ס�NEH���ó�![]() ����NH��5MP���ֲ�ͬ�������������0��t��0.3ʱ����������0.3��t��0.65ʱ����������0.65��t��1ʱ���ֱ����t�ķ�Χ�ɵó��𰸣�
����NH��5MP���ֲ�ͬ�������������0��t��0.3ʱ����������0.3��t��0.65ʱ����������0.65��t��1ʱ���ֱ����t�ķ�Χ�ɵó��𰸣�
�⣺��1����y��a��x��0.4��2+3.32��a��0����
��x��0��y��3���룬���a����2��
�������ߵĺ�������ʽΪy����2��x��0.4��2+3.32��
��2���ٰ�y��2.6����y����2��x��0.4��2+3.32��
����ã�x��0.4��2��0.36��
���x1����0.2����ȥ����x2��1��
��OD��1m��
�ڶ�����ֱ�ߴ�����Խ��С�������ش�����E��
��ͼ1�ɵã���0��t��0.3ʱ��h2��2.2��
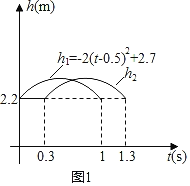
��0.3��t��1.3ʱ��h2����2��t��0.8��2+2.7��
��h1��h2��0ʱ��t��0.65��
�����ڵ�D��������С���ڵ�F�����ص�ʾ��ͼ��ͼ2��
��MD��h1��NF��h2��
����M��N��E���㹲��ʱ������E��EG��MD�ڵ�G����NF�ڵ�H������N��NP��MD�ڵ�P��
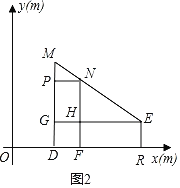
��MD��NF��PN��EG��
���M����HEN����MNP����NEH��
���MPN�ס�NEH��
��![]() ��
��
��PN��0.5��HE��2.5��
��NH��5MP��
��������0��t��0.3ʱ��
MP����2��t��0.5��2+2.7��2.2����2��t��0.5��2+0.5��
NH��2.2��1.3��0.9��
��5[��2��t��0.5��2+0.5]��0.9��
�����ã�t��0.5��2��0.16��
���![]() ����ȥ����
����ȥ����![]() ��
��
��0��t��0.3ʱ��MP��t�����������
��![]() ��
��
��������0.3��t��0.65ʱ��MP��MD��NF����2��t��0.5��2+2.7��[��2��t��0.8��2+2.7]����1.2t+0.78��
NH��NF��HF����2��t��0.8��2+2.7��1.3����2��t��0.8��2+1.4��
�ੁ2��t��0.8��2+1.4��5������1.2t+0.78����
������t2��4.6t+1.89��0��
��ã�![]() ����ȥ����
����ȥ����![]() ��
��
��0.3��t��0.65ʱ��MP��t���������С��
��![]() ��
��
��������0.65��t��1ʱ��h1��h2�������ܣ�
�������������������������ʱ�䷶ΧΪ![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�