题目内容
【题目】如图,以ABCD 的四条边为边,分别向外作正方形,连结 EF,GH,IJ,KL.如果ABCD 的 面积为 8,则图中阴影部分四个三角形的面积和为( )

A.8B.12C.16D.20
【答案】C
【解析】
连接AC,通过证明△EAF≌△ABC,可求S△EAF=![]() =4,同理求出理S△BHG= S△CIJ= S△DLK=
=4,同理求出理S△BHG= S△CIJ= S△DLK=![]() =4,即可求出阴影部分四个三角形的面积和.
=4,即可求出阴影部分四个三角形的面积和.
解:连接AC,
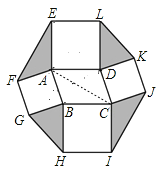
∵四边形ABGF和四边形ADLE是正方形,
∴AE=AD,AF=AB,∠FAB=∠EAD=90°,
∴∠EAF+∠BAD=360°-90°-90°=180°,
∵∠BAD+∠ABC=180°,
∴∠EAF=∠ABC,
在△EAF和△ABC中,
∵AE=AD=BC,
∠EAF=∠ABC,
AF=AB,
∴△EAF≌△ABC,
∴S△EAF≌S△ABC=![]() =4,
=4,
同理可求:S△BHG= S△CIJ= S△DLK=![]() =4,
=4,
∴阴影部分的面积S=S△AEF+S△BGH+S△CIJ+S△DLK=4×4=16.
故选:C.

练习册系列答案
相关题目