��Ŀ����
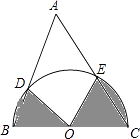
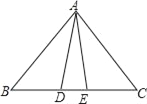
����Ŀ����ͼ���ڡ�ABC�У���BAC=90�㣬AB=AC=6��DΪBC���е㣮 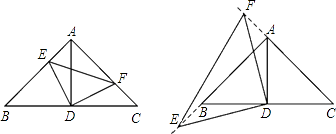
��1����E��F�ֱ���AB��AC�ϵĵ㣬��AE=CF����֤����AED�ա�CFD��
��2������F��E�ֱ��C��A����ͬʱ��������ÿ��1����λ���ȵ��ٶ���CA��AB�˶�������A��Bʱֹͣ�����DEF�����Ϊy��F���˶���ʱ��Ϊx����y��x�ĺ�����ϵʽ��
��3���ڣ�2���������£���F��E�ֱ���CA��AB���ӳ������˶������ʱy��x�ĺ�����ϵʽ��
���𰸡�
��1��֤�����ߡ�BAC=90�� AB=AC=6��DΪBC�е�
���BAD=��DAC=��B=��C=45��
��AD=BD=DC
��AE=CF���AED�ա�CFD��SAS��
��2���⣺�������У�FC=AE=x��
�ߡ�AED�ա�CFD
��S�ı���AEDF=S��AED+S��ADF=S��CFD+S��ADF=S��ADC=9
�� ![]() S�ı���AEDF-
S�ı���AEDF- ![]()
�� ![]() ��
��
��3���⣺�������У�AF=BE=x��6��AD=DB����ABD=��DAC=45��
���DAF=��DBE=135��
���ADF�ա�BDE
��S��ADF=S��BDE
��S��EDF=S��EAF+S��ADB
= ![]()
�� ![]() ��
��

����������1�����õ���ֱ�������ε����ʵõ���BAD=��DAC=��B=��C=45�㣬�����õ�AD=BD=DC��Ϊ֤����AED�ա�CFD�ṩ����Ҫ����������2������S�ı���AEDF=S��AED+S��ADF=S��CFD+S��ADF=S��ADC=9 ���ɵõ�y��x֮��ĺ�����ϵʽ����3���������У�AF=BE=x��6��AD=DB����ABD=��DAC=45��õ���DAF=��DBE=135�㣬�Ӷ��õ���ADF�ա�BDE������ȫ�������������ȵõ�S��ADF=S��BDE�Ӷ��õ�S��EDF=S��EAF+S��ADB����ȷ����������֮��ĺ�����ϵʽ��
�����㾫�������ڱ��⿼��ĵ���ֱ�������Σ���Ҫ�˽����ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45����ܵó���ȷ�𰸣�