题目内容
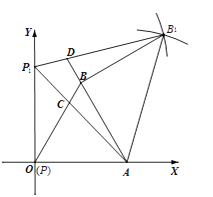
【题目】如图,已知∠XOY=90°,等边三角形PAB的顶点P与O点重合,顶点A是射线OX上的一个定点,另一个顶点B在∠XOY的内部. 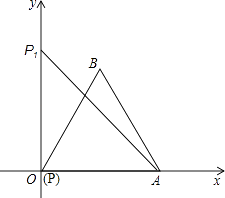
(1)当顶点P在射线OY上移动到点P1时,连接AP1 , 请用尺规作图;在∠XOY内部作出以AP1为边的等边△AP1B1(要求保留作图痕迹,不要求写作法和证明);
(2)设AP1交OB于点C,AB的延长线交B1P1于点D.求证:△ABC∽△AP1D;
(3)连接BB1 , 求证:∠ABB1=90°.
【答案】
(1)解:等边三角形作图所如下;

(2)∵△PAB、△P1AB1是等边三角形,
∴∠ABC=∠AP1D=60°,
又∵∠BAC=∠P1AD,
∴△ABC∽△AP1D.
(3)证明:
∵△PAB、△P1AB1是等边三角形,
∴∠BAP=∠P1AB1=60°,AB=AP,AB1=AP1.
∴∠BA B1=∠P1AP.
∴△BA B1≌△P1AP(SAS).
∴∠AB B1=∠P1 PA=90°.
【解析】(1)分别以A、P1为圆心,AP1长为半径画弧,两弧交于B1点,△AP1B1即为所求;(2)欲证△ABC∽△AP1D,必须有两组角相等,∠BAC=∠P1AD为一个公共角,又因为△PAB和△P1AB1都是正三角形,所以有∠ABC=∠AP1D=60°所以△ABC∽△AP1D;(3)有(1)(2)可知AO=AB,AP1=AB1 , ∠PAB=∠P1AB1=60°,所以有∠OAP1=∠BAB1=60°﹣∠CAB,因此根据边角边公式可证△OAP1≌△BAB1 , 因此可得∠ABB1=∠AOP1=90°
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 名校课堂系列答案
名校课堂系列答案