题目内容
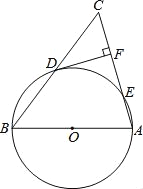
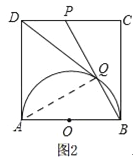
【题目】如图,在正方形ABCD中,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ.给出如下结论:
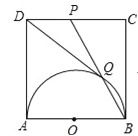
①DQ与半圆O相切;②![]() ;③∠ADQ=2∠CBP;④cos∠CDQ=
;③∠ADQ=2∠CBP;④cos∠CDQ=![]() .其中正确的是 (请将正确结论的序号填在横线上).
.其中正确的是 (请将正确结论的序号填在横线上).
【答案】①③
【解析】
试题解析:①如图1
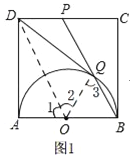
连接DO,OQ,在正方形ABCD中,AB∥CD,AB═CD,
∵P是CD中点,O是AB中点,
∴DP∥OB,DP═OB,
∴四边形OBDP是平行四边形,
∴OD∥BP,
∴∠1=∠OBQ,∠2=∠3,
又∵OQ=OB,
∴∠3=∠OBQ,
∴∠1=∠2,
在△AOD和△QOD中,
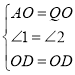 ,
,
∴△AOD≌△QOD,
∴∠OQD=∠A=90°,
∴DQ与半圆O相切,
①正确;
②如图2
连接AQ,可得:∠AQB=90°,
在正方形ABCD中,AB∥CD,
∴∠ABQ=∠BPC,
设正方形边长为x,则CP=![]() x,
x,
由勾股定理可求:BP=![]() ,
,
∴cos∠BPC=![]() ,cos∠ABQ=
,cos∠ABQ=![]() ,
,
∴![]() =
=![]() ,又AB=x,
,又AB=x,
可求,BQ=![]() x,
x,
PQ=![]() x,
x,
∴![]() ,
,
②不对;
③如图3

连接AQ,OQ,
由①知,∠OQD=90°,又∠OAD=90°,可求∠ADQ+∠AOQ=180°,
∵∠3+∠AOQ=180°,
∴∠3=∠ADQ,
由②知,∠1+∠4=90°,
又∠4+∠CBP=90°,
∴∠CBP=∠1,
∵OA=OQ,
∴∠1=∠2,
又∵∠3=∠1+∠2,
∴∠3=2∠CBP,
∴∠ADQ=2∠CBP,
故③正确;
④如图4,

过点Q作QH⊥CD,
易证QH∥BC,
设正方形边长为x,由②知:PQ=![]() x,cos∠BPC=
x,cos∠BPC=![]() ,
,
可求:PH=![]() x,HQ=
x,HQ=![]() x,
x,
∴DH=DP+PH=![]() x,
x,
由勾股定理可求:DQ=x,
∴cos∠CDQ=![]() ,
,
故④不正确.
综上所述:正确的有①③.

练习册系列答案
相关题目