题目内容
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,DF⊥AC于F.
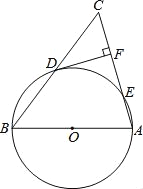
(1)求证:DF为⊙O的切线;
(2)若cosC=![]() ,CF=9,求AE的长.
,CF=9,求AE的长.
【答案】(1)证明见解析;(2)7.
【解析】
试题分析:(1)连接OD,AD,求出OD∥AC,推出OD⊥DF,根据切线的判定推出即可;
(2)求出CD、DF,推出四边形DMEF和四边形OMEN是矩形,推出OM=EN,EM=DF=12,求出OM,即可求出答案.
试题解析:(1)连接OD,AD,
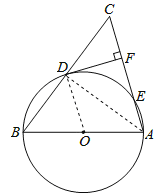
∵AB是⊙的直径,
∴∠ADB=90°,
又∵AB=AC,
∴BD=CD
又∵OB=OA,
∴OD∥AC
∵DF⊥AC,
∴OD⊥DF
又∵OD为⊙的半径,
∴DF为⊙O的切线.
(2)连接BE交OD于M,过O作ON⊥AE于N,
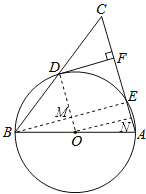
则AE=2NE,
∵cosC=![]() ,CF=9,
,CF=9,
∴DC=15,
∴DF=![]() =12,
=12,
∵AB是直径,
∴∠AEB=∠CEB=90°,
∵DF⊥AC,OD⊥DF,
∴∠DFE=∠FEM=∠MDF=90°,
∴四边形DMEF是矩形,
∴EM=DF=12,∠DME=90°,DM=EF,
即OD⊥BE,
同理四边形OMEN是矩形,
∴OM=EN,
∵OD为半径,
∴BE=2EM=24,
∵∠BEA=∠DFC=90°,∠C=∠C,
∴△CFD∽△CEB,
∴![]() ,
,
∴![]() ,
,
∴EF=9=DM,
设⊙O的半径为R,
则在Rt△EMO中,由勾股定理得:R2=122+(R-9)2,
解得:R=![]() ,
,
则EN=OM=![]() -9=
-9=![]() =
=![]() ,
,
∴AE=2EN=7.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目