Question

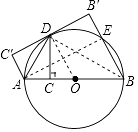
【题目】如图，AB是⊙O的直径，点C为AB上一点，作CD⊥AB交⊙O于D，连接AD，将△ACD沿AD翻折至△AC′D．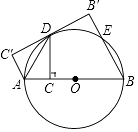

（1）请你判断C′D与⊙O的位置关系，并说明理由；
（2）过点B作BB′⊥C′D′于B′，交⊙O于E，若CD= ，AC=3，求BE的长．

Answer 1

【答案】
（1）解：C′D是⊙O的切线，

理由：连接OD，

∵OD=OA，

∴∠OAD=∠ADO，

∵将△ACD沿AD翻折至△AC′D，

∴∠C′DA=∠CDA，

∵CD⊥AB，

∴∠DAC+∠ADC=90°，

∴∠ADO+∠C′DA=90°，

∴OD⊥C′D，

∴C′D是⊙O的切线

（2）解：连接AE，BD，

∵AB是⊙O的直径，

∴AE⊥BE，AD⊥BD，

∵BB′⊥C′D′，

∴∠C′=∠B′=∠AEB′=90°，

∴四边形AEB′C′是矩形，

∴AC′=B′E，AE=C′B′，

∵将△ACD沿AD翻折至△AC′D，

∵AC′=AC=3，C′D=CD= ，

∵AC′⊥C′B′，OD⊥C′B′，

∴AC′∥OD∥BB′，

∵AO=BO，

∴C′B′=2C′D=2 ，

∴AE=2 ，

∵DC⊥AB，

∴CD2=ACCB，

∴CB=7，

∴AB=10，

∴BE= =4．

【解析】（1）连接OD，根据等腰三角形的性质得到∠OAD=∠ADO，根据折叠的性质得到∠C′DA=∠CDA，于是得到结论；
（2）连接AE，BD，由AB是⊙O的直径，得到AE⊥BE，AD⊥BD，推出四边形AEB′C′是矩形，得到AC′=B′E，AE=C′B′，根据折叠的性质得到AC′=AC=3，C′D=CD=，根据平行线等分线段定理得到AO=BO，得到AE的值，根据射影定理得到CB=7，由勾股定理即可得到BE的长．
【考点精析】认真审题，首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)，还要掌握垂径定理(垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧)的相关知识才是答题的关键．