题目内容
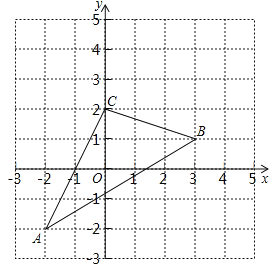
【题目】如图,已知直线y=x+k和双曲线y= ![]() (k为正整数)交于A,B两点.
(k为正整数)交于A,B两点.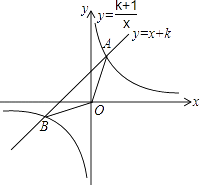
(1)当k=1时,求A、B两点的坐标;
(2)当k=2时,求△AOB的面积;
(3)当k=1时,△OAB的面积记为S1 , 当k=2时,△OAB的面积记为S2 , …,依此类推,当k=n时,△OAB的面积记为Sn , 若S1+S2+…+Sn= ![]() ,求n的值.
,求n的值.
【答案】
(1)解:当k=1时,直线y=x+k和双曲线y= ![]() 化为:y=x+1和y=
化为:y=x+1和y= ![]() ,
,
解 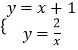 得
得 ![]() ,
, ![]() ,
,
∴A(1,2),B(﹣2,﹣1)
(2)解:当k=2时,直线y=x+k和双曲线y= ![]() 化为:y=x+2和y=
化为:y=x+2和y= ![]() ,
,
解 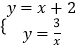 得
得 ![]() ,
, ![]() ,
,
∴A(1,3),B(﹣3,﹣1)
设直线AB的解析式为:y=mx+n,
∴ ![]()
∴ ![]() ,
,
∴直线AB的解析式为:y=x+2
∴直线AB与y轴的交点(0,2),
∴S△AOB= ![]() ×2×1+
×2×1+ ![]() ×2×3=4;
×2×3=4;
(3)解:当k=1时,S1= ![]() ×1×(1+2)=
×1×(1+2)= ![]() ,
,
当k=2时,S2= ![]() ×2×(1+3)=4,
×2×(1+3)=4,
…
当k=n时,Sn= ![]() n(1+n+1)=
n(1+n+1)= ![]() n2+n,
n2+n,
∵S1+S2+…+Sn= ![]() ,
,
∴ ![]() ×(
×( ![]() …+n2)+(1+2+3+…n)=
…+n2)+(1+2+3+…n)= ![]() ,
,
整理得: ![]() ,
,
解得:n=6.
【解析】(1)两图像的交点就是求联立的方程组的解;(2)斜三角形△AOB的面积可转化为两水平(或竖直)三角形(有一条边为水平边或竖直边的三角形称为水平或竖直三角形)的面积和或差;(3)利用n个数的平方和公式和等差数列的和公式可求出.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目