题目内容
【题目】如图,等边△DEF的顶点在等边△ABC的边上.

(1)求证:BE=CD;
(2)若BD=2CD,求∠DFC的度数.
【答案】(1)见解析;(2)∠FDC=90°
【解析】
(1)欲证明BE=CD,只要证明△BDE≌△CFD(AAS)即可;
(2)取BD的中点M,连接EM.首先证明△BEM是等边三角形,由EM=BM=DM推出∠DEB=90°,求出∠BDE即可解决问题;
(1)证明:∵△ABC,△DEF都是等边三角形,
∴∠B=∠C=∠EDF=60°,DE=DF,
∵∠EDC=∠B+∠BED=∠EDF+∠CDF,
∴∠BED=∠CDF,
∴△BDE≌△CFD(AAS),
∴BE=CD.
(2)解:取BD的中点M,连接EM.
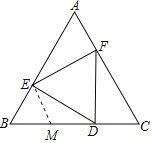
∵BD=2CD,BE=CD,
∴BD=2BE,
∵BM=MD,
∴BE=BM,
∵∠B=60°,
∴△BME是等边三角形,
∴EM=BM=MD,
∴∠BED=90°,
∴∠EDB=30°,
∴∠FDC=180°﹣30°﹣60°=90°.

练习册系列答案
相关题目
【题目】某公司实行年工资制,职工的年工资由基础工资、住房补贴和医疗费三项组成,具体规定如下:
项目 | 第一年的工资(万元) | 一年后的计算方法 |
基础工资 | 1 | 每年的增长率相同 |
住房补贴 | 0.04 | 每年增加0.04 |
医疗费 | 0.1384 | 固定不变 |
(1)设基础工资每年增长率为x,用含x的代数式表示第三年的基础工资为 万元;
(2)某人在公司工作了3年,他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18 %,问基础工资每年的增长率是多少?