题目内容
【题目】如图在给定的一张平行四边形纸片上作一个菱形,甲、乙两人的作法如下: 甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠BAD,∠ABC的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法请分别做出判断,并证明.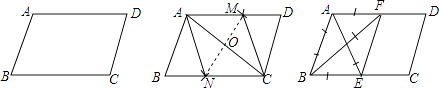
【答案】解:甲、乙做法都正确. 甲做法:
证明:∵MN垂直平分AC,
∴AO=CO,∠AOM=90°,
又∵AD∥BC,
∴∠MAC=∠NCA,
在△AOPM和△CON中,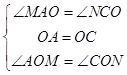 ,
,
∴△AOPM≌△CON,
∴OM=ON,
∴AC和MN互相垂直平分,
∴四边形ANCM是菱形;
乙做法:
证明:∵AE平分∠BAD,
∴∠BAE=∠EAF,
又∵AD∥BC,
∴∠EAF=∠BEA,
∴∠BAE=∠BEA
∴AB=BE,
同理可得AB=AF,
∴BE=AF,
∵BE∥AF,
∴四边形ABEF为平行四边形
又∵AB=BE,
∴四边形ANCM是菱形
【解析】对于甲做法:利用MN垂直平分AC得到AO=CO,∠AOM=90°,再由AD∥BC得到∠MAC=∠NCA,则可证明△AOPM≌△CON,所以OM=ON,于是根据菱形的判定方法可判断四边形ANCM是菱形; 对于乙做法:由AE平分∠BAD得到∠BAE=∠EAF,再由AD∥BC得到∠EAF=∠BEA,则∠BAE=∠BEA,所以AB=BE,同理可得AB=AF,所以BE=AF,于是可证明四边形ABEF为平行四边形,再加上邻边相等可判断四边形ANCM是菱形.
【考点精析】本题主要考查了菱形的判定方法的相关知识点,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】某商场试销一种新款衬衫,一周内销售情况如下表所示:
型号(厘米) | 38 | 39 | 40 | 41 | 42 | 43 |
数量(件) | 25 | 30 | 36 | 50 | 28 | 8 |
商场经理要了解哪种型号最畅销,则上述数据的统计量中,对商场经理来说最有意义的是( )
A.平均数 B.众数C.中位数D.方差
【题目】在洋浦一新开业的以经营男式皮鞋为主的鞋店当服务员的阿丽是个做事善于观察的小姑娘,上班一段时间后,她发现各种尺码的男式皮鞋销量并不均衡,于是她把这个发现记录下来交给了她的老板:
尺码 | 37 | 38 | 39 | 40 | 41 | 42 | 43 |
销量(双) | 12 | 15 | 22 | 28 | 32 | 30 | 4 |
你认为这个销售记录对老板管理鞋店生意有用吗?如果你认为有用,请说明你的理由,并请你帮这个老板策划一下如何利用这些信息?