��Ŀ����
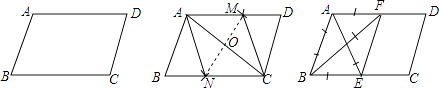
����Ŀ��һ�����ǰ�������ڽǷֱ���90�㣬45�㣬45���90�㣬60�㣬30�㣬����ͼ��ʾ������һ�����̶�������AOB���ı�������ACD��λ�ã����е�Aλ��ʼ�ղ��䣩�����ڳɲ�ͬ��λ�ã�ʹ�������ǰ�������һ���ƽ�У����BAD=����0�㣼����180�㣩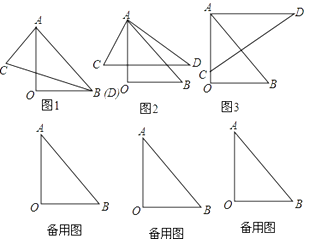
��1����ͼ2�У�����̽������Ϊ����ʱ��CD��OB����˵�����ɣ�
��2����ͼ3�У�����=ʱ��AD��OB��
��3���ڵ�Aλ��ʼ�ղ��������£��㻹�ܰڳɼ��ֲ�ͬ��λ�ã�ʹ�������ǰ���������һ���ƽ�У���ֱ��д������Ҫ��Ħ��Ķ�����
���𰸡�
��1��
�⣺��ͼ2��
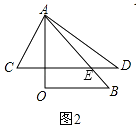
��CD��OB��
���AEC=��B=45�㣬
�ߡ�D=30�㣬
���=��BAD=45�㩁30��=15�㣬
�൱��=15��ʱ��CD��OB
��2��45��
��3��
�⣺����ͼ4��

��CD��OA��
���D+��DAO=180��
���BAD=180�㩁45�㩁30��=105�㣬
�൱��=105��ʱ��CD��OA��
����ͼ5��
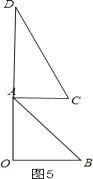
��AC��OB��
���CAB=��B=45�㣬
���BAD=��CAB+��CAD=45��+90��=135�㣬
�൱��=135��ʱ��AC��OB��
����ͼ6��
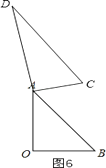
��DC��AB��
���C=��BAC=60��
���BAD=90��+60��=150�㣬
�൱��=150��ʱ��DC��AB��
����ͼ7������BC��
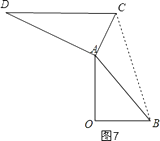
��DC��OB��
���DCB+��OBC=180�㣬
�ߡ�ACD=60�㣬��OBA=45�㣬
���ACB+��ABC=180�㩁60�㩁45��=75�㣬
���CAB=105�㣬
���BAD=360�㩁90�㩁105��=165�㣬
�൱��=165��ʱ��CD��OB��
����ͼ8��

��AD��OB��
���DAO=��O=90�㣬
���BAD=90��+45��=135�㣬
�൱��=135��ʱ��AD��OB��
����ͼ9��
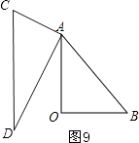
��CD��OA��
���D=��DAO=30�㣬
���BAD=30��+45��=75�㣬
�൱��=75��ʱ��CD��OA��
����ͼ10��
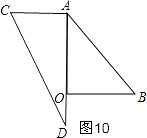
��AC��OB��
��AO��AD�غϣ�
���BAD=45�㣬
�൱��=45��ʱ��AC��OB��
����ͼ11��
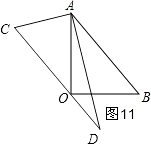
��OC��AB��
���BAD=��D=30�㣬
�൱��=30��ʱ��OC��AB��
���������⣺��2����ͼ3����AD��OB��
���BAD=��B=45�㣬
�൱��=45��ʱ��AD��OB��
���Դ��ǣ�45�㣻
�����㾫��������ͬλ�ǡ��ڴ��ǡ�ͬ���ڽǶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪����ֱ�߱�������ֱ�������γɰ˸��ǣ����ǹ�����ͬλ�ǡ��ڴ�����ͬ���ڽ�;�б�ͬλ�ǡ��ڴ��ǻ�ͬ���ڽǵĹؼ����ҵ������������ǵġ����ߡ�����ʱ��Ҫ���йصIJ��֡����������ص�����ȥ��������ʱ����Ҫ��ͼ�β�ȫ��