题目内容
【题目】一次函数y=kx+b图象经过点(0,3)和(4,7).
①试求k与b;
②画出这个一次函数图象;
③这个一次函数与x轴交点坐标是_____;
④当x_____时,y<0;
⑤当x_____时,y>0;
⑥当0<y<7时,x的取值范围是_____.
【答案】①k=1,b=3;②图象见解析;③(-3,0);④<-3;⑤>-3;⑥-3.
【解析】试题分析:①将(0,3)和(4,7)分别代入代入y=kx+b,联立解方程可得k和b的值;
②根据函数经过(0,3)和(4,7)两点可确定函数图象;
③根据(1)所求的解析式令y=0即可求出与x轴交点的坐标;
④观察图象即可得;
⑤观察图象即可得;
⑥将y=0、y=7分别代入(1)中的解析式即可得.
试题解析:①把点(0,3)和(4,7)代入y=kx+b得![]() ,解得
,解得![]() ;
;
②函数的图象如图:
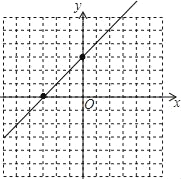
③由①可知:y=x+3,令y=0,则有x+3=0,解得:x=-3,所以图象与x轴的交点坐标为(﹣3,0),
故答案为:(-3,0);
④观察图象可知当x<﹣3时,y<0,
故答案为<-3;
⑤观察图象可知当x>﹣3时,y>0,
故答案为>-3;
⑥y=0时,0=x+3,解得:x=-3,
y=7时,7=x+3,解得:x=4,
所以当0<y<7时,x的取值范围是﹣3<x<4,
故答案为:﹣3<x<4.

练习册系列答案
相关题目