��Ŀ����
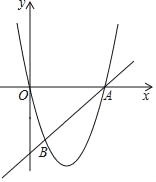
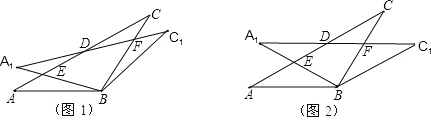
����Ŀ�����������������й���ͳ��ѧ����Ҫ����������������������������һ�����⣺�������ط����ٲ������п��ţ�������ʮ�岽��ľ���ʣ������ż������ľ�����ý���Ļ�˵�������ǣ���ͼ��DEFG��һ���߳�Ϊ200�����������ǹŴ��ij��ȵ�λ����������С�ǣ�����Hλ��GD���е㣬����Kλ��ED���е㣬������15����A����һ��ľ��������Ŷ��ٲ�ǡ�ÿ���λ��A������ľ������D��ֱ��AC�ϣ����������KC�ij�Ϊ���ٲ���

���𰸡�![]()
��������
����ƽ��֤����CDK�ס�DAH���������Ʊȼ��ɵó���.
�⣺DH=100��DK=100��AH=15��
��AH��DK��
���CDK=��A��
����CKD=��AHD��
���CDK�ס�DAH��
��![]() ����
����![]() ��
��
��CK=![]()
��KC�ij�Ϊ![]() ����
����

����Ŀ���ס�������ͬѧ����һ�����������ϲ��ԣ����ֱ��涨����6������![]() ��6��
��6��![]() Ϊ�ϸ���9������
Ϊ�ϸ���9������![]() ��9��
��9��![]() Ϊ���㣬����ͬѧ�IJ��Գɼ����±���
Ϊ���㣬����ͬѧ�IJ��Գɼ����±���
�ɼ� | ��4 | ��5 | ��6 | ��7 | ��8 | ��9 |
������ | ��1 | ��2 | ��5 | ��2 | ��1 | ��4 |
������ | ��1 | ��1 | ��4 | ��5 | ��2 | ��2 |
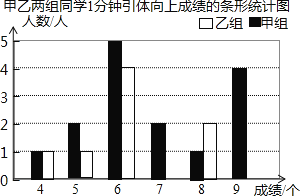
�ֽ�����ͬѧ�IJ��Գɼ����Ƴ����²�������ͳ��ͼ����
ͳ���� | ƽ���� | ��λ�� | ���� | ���� | �ϸ��� | ������ |
���� | a | 6 | 6 |
|
|
|
���� |
| b | 7 |
|
|
|
![]() ������ͳ��ͼ����������
������ͳ��ͼ����������
![]() ͳ�Ʊ��е�
ͳ�Ʊ��е�![]() ______��
______��![]() ______��
______��
![]() ��˵����������ʸ������������ʣ����Լ���ɼ�������ɼ��ã���Ҳ����˵����ɼ��ȼ���ɼ��ã������������֧������ɼ��õ����ɣ�
��˵����������ʸ������������ʣ����Լ���ɼ�������ɼ��ã���Ҳ����˵����ɼ��ȼ���ɼ��ã������������֧������ɼ��õ����ɣ�
����Ŀ��ijС�ͼӹ�����ÿ�������ס����������͵IJ�Ʒ��1000����ԭ�ϳɱ������۵��ۣ������˼Ƽ����������
�ף�Ԫ/���� | �ң�Ԫ/���� | |
ԭ�ϳɱ� | 10 | 8 |
���۵��� | 20 | 16 |
�Ƽ����� | 2 | 1.5 |
��üӹ���ÿ���������Ͳ�Ʒx����ÿ����������ΪyԪ��
��1�����y��x֮��ĺ�����ϵʽ��
��2�����ù���ÿ��Ͷ���ܳɱ�������10750Ԫ���������żס����������͵�����������ʹ�ó�ÿ������õ�������������������ܳɱ���ԭ�ϳɱ�+�Ƽ����ʣ�������������һͶ���ܳɱ���