题目内容
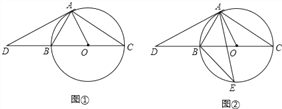
【题目】已知BC是⊙O的直径,AD是⊙O的切线,切点为A,AD交CB的延长线于点D,连接AB,AO.
(1)如图①,求证:∠OAC=∠DAB;
(2)如图②,AD=AC,若E是⊙O上一点,求∠E的大小.
【答案】(1)证明见解析;(2)30°.
【解析】试题分析:(Ⅰ)先由切线和直径得出直角,再用同角的余角相等即可;
(Ⅱ)由等腰三角形的性质和圆的性质直接先判断出![]() ,即可求出
,即可求出![]() .
.
试题解析:(Ⅰ)∵AD是![]() 的切线,切点为A,
的切线,切点为A,
∴DA⊥AO,
∴![]()
∴![]()
∵BC是![]() 的直径,
的直径,
∴![]()
∴![]()
∴∠OAC=∠DAB,
(Ⅱ)∵OA=OC,
∴∠OAC=∠C,
∵AD=AC,
∴∠D=∠C,
∴∠OAC=∠D,
∵∠OAC=∠DAB,
∴∠DAB=∠D,
∵∠ABC=∠D+∠DAB,
∴∠ABC=2∠D,
∵∠D=∠C,
∴∠ABC=2∠C,
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
【题目】为了解某校七年级男生的身高(单位:![]() )情况,随机抽取了七年级部分学生进行了抽样调查.统计数据如下表:
)情况,随机抽取了七年级部分学生进行了抽样调查.统计数据如下表:
组别 |
|
|
|
|
|
身高 |
|
|
|
|
|
人数 |
|
|
|
|
|
(1)样本容量是多少?组距是多少?组数是多少?
(2)画出适当的统计图表示上面的信息;
(3)若全校七年级学生有![]() 人,请估计身高不低于
人,请估计身高不低于![]() 的学生人数.
的学生人数.