题目内容
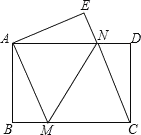
【题目】如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3:1,ND=1.
①求MC的长.
②求MN的长.
【答案】(1)证明见解析;(2)①MC=3;②MN=2![]() .
.
【解析】
(1)根据折叠可得∠AMN=∠CMN,再根据平行可得∠ANM=∠CMN,可证CM=CN
(2)①根据等高的两个三角形的面积比等于边的比,可求MC的长.
②作NF⊥MC,可得矩形NFCD,根据勾股定理可求CD,则可得NF,MF,再根据勾股定理可求MN的长.
解:(1)∵折叠
∴CM=AM,CN=AN,∠AMN=∠CMN
∵ABCD是矩形
∴AD∥BC
∴∠ANM=∠CMN
∴∠ANM=∠AMN
∴CM=CN
(2)①∵AD∥BC
∴△CMN和△CDN是等高的两个三角形
∴S△CMN:S△CDN=3:1=CM:DN且DN=1
∴MC=3
②∵CM=CN
∴CN=3且DN=1
∴根据勾股定理 CD=2![]()
如图作NF⊥MC
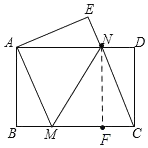
∵NF⊥MC,∠D=∠DCB=90°
∴NFCD是矩形
∴NF=CD=2![]() ,FC=DN=1
,FC=DN=1
∴MF=2
在Rt△MNF中,MN=![]() =2
=2![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目