题目内容
已知:在等腰梯形ABCD中,AD∥BC,直线MN是梯形的对称轴,P是MN上的一点.直线BP交直线DC于F,交CE于E,且CE∥AB.
(1)若点P在梯形的内部,如图①.求证:BP2=PE•PF;
(2)若点P在梯形的外部,如图②,那么(1)的结论是否成立?若成立,请证明;若不成立,请说明理由.
(1)若点P在梯形的内部,如图①.求证:BP2=PE•PF;
(2)若点P在梯形的外部,如图②,那么(1)的结论是否成立?若成立,请证明;若不成立,请说明理由.

(1)证明:连接PC,
直线MN是等腰梯形ABCD的对称轴,
∴BP=CP,∠PBC=∠PCB,∠ABC=∠DCB,
∵CE∥AB
∴∠E=∠ABE
∴∠PCD=∠E
∵∠FPC=∠FPC
∴△PCF∽△PEC
∴PC:PE=PF:PC
∴BP2=PE•PF;
(2)成立.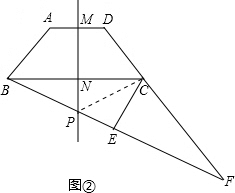
连接PC,
理由:直线MN是等腰梯形ABCD的对称轴,
∴BP=CP,∠PBC=∠PCB,∠ABC=∠DCB,
∵CE∥AB,
∴∠CEF=∠ABE,
∴∠ABC=∠BCE,∠PCE=∠BCE-∠BCP=∠ABC-∠CBP=∠DCB-∠CBP=∠F,即∠F=∠DCB-∠CBF,
∵∠FPC=∠FPC,
∴△PCF∽△PEC,
∴PC:PE=PF:PC,
∴BP2=PE•PF.

直线MN是等腰梯形ABCD的对称轴,
∴BP=CP,∠PBC=∠PCB,∠ABC=∠DCB,
∵CE∥AB
∴∠E=∠ABE
∴∠PCD=∠E
∵∠FPC=∠FPC
∴△PCF∽△PEC
∴PC:PE=PF:PC
∴BP2=PE•PF;
(2)成立.

连接PC,
理由:直线MN是等腰梯形ABCD的对称轴,
∴BP=CP,∠PBC=∠PCB,∠ABC=∠DCB,
∵CE∥AB,
∴∠CEF=∠ABE,
∴∠ABC=∠BCE,∠PCE=∠BCE-∠BCP=∠ABC-∠CBP=∠DCB-∠CBP=∠F,即∠F=∠DCB-∠CBF,
∵∠FPC=∠FPC,
∴△PCF∽△PEC,
∴PC:PE=PF:PC,
∴BP2=PE•PF.


练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目





 =2,BC=8.
=2,BC=8.