ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΈ ΧβΧΫΨΩΘΚ
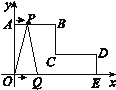
Θ®1Θ©»γΆΦΔΌΘ§±Ώ≥ΛΈΣ4ΒΡΒ»±ΏΓςOABΈΜ”ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΫΪΓςOAB’έΒΰΘ§ ΙΒψB¬δ‘ΎOAΒΡ÷–Βψ¥ΠΘ§‘ρ’έΚέ≥ΛΈΣΘΜ
Θ®2Θ©»γΆΦΔΎΘ§ΨΊ–ΈOABCΈΜ”ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Τδ÷–OA=8Θ§AB=6Θ§ΫΪΨΊ–Έ―ΊœΏΕΈMN’έΒΰΘ§ΒψB¬δ‘Ύx÷α…œΘ§Τδ÷–AN= ![]() ABΘ§«σ’έΚέMNΒΡ≥ΛΘΜ
ABΘ§«σ’έΚέMNΒΡ≥ΛΘΜ
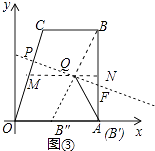
Θ®3Θ©»γΆΦΔέΘ§ΥΡ±Ώ–ΈOABCΈΜ”ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Τδ÷–OA=AB=6Θ§CB=4Θ§BCΓΈOAΘ§ABΓΆOA”ΎΒψAΘ§ΒψQΘ®4Θ§3Θ©ΈΣΥΡ±Ώ–ΈΡΎ≤Ω“ΜΒψΘ§ΫΪΥΡ±Ώ–Έ’έΒΰΘ§ ΙΒψB¬δ‘Ύx÷α…œΘ§Έ «Ζώ¥φ‘ΎΙΐΒψQΒΡ’έΚέΘ§»τ¥φ‘ΎΘ§«σ≥ω’έΚέ≥ΛΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°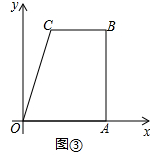
ΓΨ¥πΑΗΓΩ
Θ®1Θ©2
Θ®2Θ©
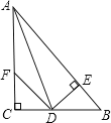
ΫβΘΚ»γΆΦ2÷–Θ§BΒΡΕ‘≥ΤΒψBΓδΘ§’έΚέΈΣMNΘ§MNΫΜBBΓδ”ΎH
ΓΏAN= ![]() AB=2Θ§
AB=2Θ§
ΓύNB=NBΓδ=4Θ§
‘ΎRtΓςANBΓδ÷–Θ§ABΓδ= ![]() =2
=2 ![]() Θ§
Θ§
ΓύOBΓδ=8©¹2 ![]() Θ§
Θ§
ΓύΒψBΓδΘ®8©¹2 ![]() Θ§0Θ©Θ§
Θ§0Θ©Θ§
ΓΏBΘ®8Θ§6Θ©Θ§
ΓύBBΓδ÷–ΒψHΘ®8©¹ ![]() Θ§3Θ©Θ§ΓΏΒψNΉχ±ξΘ®8Θ§2Θ©Θ§
Θ§3Θ©Θ§ΓΏΒψNΉχ±ξΘ®8Θ§2Θ©Θ§
…η÷±œΏNHΫβΈω ΫΈΣy=kx+bΘ§‘ρ”– ![]() ΫβΒΟ
ΫβΒΟ 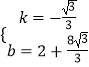 Θ§
Θ§
Γύ÷±œΏNHΫβΈω ΫΈΣy=©¹ ![]() x+2+
x+2+ ![]() Θ§
Θ§
ΓύΒψMΉχ±ξΘ®0Θ§2+ ![]() Θ©Θ§
Θ©Θ§
ΓύMN= ![]() =
= ![]()
Θ®3Θ©
ΫβΘΚ¥φ‘ΎΘ°
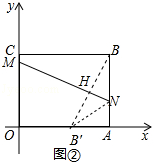
άμ”…ΘΚ»γΆΦ3÷–Θ§―”≥ΛBQΫΜOA”ΎBΓεΘ§Ν§Ϋ”AQΘ§ΙΐΒψQΉςMNΓΈOAΘ§ΫΜOC”ΎMΘ§ΫΜAB”ΎNΘ°
ΓΏQΘ®4Θ§3Θ©Θ§
ΓύNΘ®6Θ§3Θ©Θ§
ΓύBN=ANΘ°QB=QBΓεΘ§
ΉςBBΓεΒΡ¥Ι÷±ΤΫΖ÷œΏPFΘ§ΫΜOC”ΎPΘ§ΫΜAB”ΎFΘ§¥Υ ±BΓΔBΓεΙΊ”Ύ÷±œΏPFΕ‘≥ΤΘ§¬ζΉψΧθΦΰΘ§
‘ΎRtΓςABBΓε÷–Θ§ΓΏΓœBABΓε=90ΓψΘ§BQ=QBΓεΘ§
ΓύAQ=QBΘ§
Γύ¥Υ ±BΓΔAΘ®BΓδΘ©ΙΊ”Ύ÷±œΏMNΕ‘≥ΤΘ§¬ζΉψΧθΦΰΘ°
ΓΏCΘ®2Θ§6Θ©Θ§
Γύ÷±œΏOCΫβΈω ΫΈΣy=3xΘ§
ÿNMøOAȧBN=NAȧ
ΓύCM=OMΘ§
ΓύΒψMΘ®1Θ§3Θ©Θ§
ΓύMN=5Θ®ΙΐMΉωMM'ΓΆBA”ΎM'Θ§άϊ”ΟΓςBB'A÷–AB'=2ΓΧ3Θ§AB=6Θ§Υυ“‘ΓœB'BA=30ΓψΘ§ΫχΕχΆΤΒΦΓœM'MN=30ΓψΘ§«σΒΟMNΫαΙϊΗϋΩλΘΓΘ©
ΓΏBΘ®6Θ§6Θ©Θ§BΓεΘ®2Θ§0Θ©Θ§
ΓύΩ…ΒΟ÷±œΏBBΓεΒΡΫβΈω ΫΈΣy= ![]() x©¹3Θ§
x©¹3Θ§
ΓύΙΐΒψQ¥Ι÷±BBΓεΒΡ÷±œΏPFΒΡΫβΈω ΫΈΣy=©¹ ![]() x+
x+ ![]() Θ§
Θ§
”… 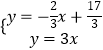 ΫβΒΟ
ΫβΒΟ 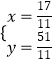 Θ§
Θ§
ΓύΒψPΘ® ![]() Θ§
Θ§ ![]() Θ©Θ§FΘ®6Θ§
Θ©Θ§FΘ®6Θ§ ![]() Θ©Θ§
Θ©Θ§
ΓύPF= ![]() =
= ![]() Θ§
Θ§
Ήέ…œΥυ ωΘ§’έΚέΒΡ≥ΛΈΣ5Μρ ![]()
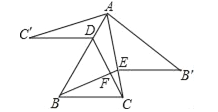
ΓΨΫβΈωΓΩΫβΘΚΘ®1Θ©»γΆΦ1÷–Θ§BΒΡΕ‘≥ΤΒψBΓδΘ§’έΚέΈΣMNΘ§MNΫΜBBΓδ”ΎHΘ°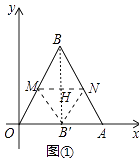
ΓΏΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§OBΓδ=BΓδAΘ§
ΓύBBΓδΓΆOAΘ§”÷ΓΏBBΓδΓΆMNΘ§
ΓύMNΓΈOAΘ§ΓΏBH=HBΓδΘ§
ΓύBM=OMΘ§BN=NAΘ§
ΓύMN «ΓςABCΒΡ÷–ΈΜœΏΘ§
ΓύMN= ![]() OA=2Θ°
OA=2Θ°
Ι ¥πΑΗΈΣ2Θ°
Θ®1Θ©»γΆΦ1÷–Θ§BΒΡΕ‘≥ΤΒψBΓδΘ§’έΚέΈΣMNΘ§MNΫΜBBΓδ”ΎHΘ°÷Μ“Σ÷ΛΟς’έΚέ «ΓςABCΒΡ÷–ΈΜœΏΦ¥Ω…Θ°Θ®2Θ©»γΆΦ2÷–Θ§BΒΡΕ‘≥ΤΒψBΓδΘ§’έΚέΈΣMNΘ§MNΫΜBBΓδ”ΎHΘ§«σ≥ω÷±œΏMNΒΡΫβΈω ΫΦ¥Ω…ΫβΨωΈ ΧβΘ°Θ®3Θ©¥φ‘ΎΘ°»γΆΦ3÷–Θ§―”≥ΛBQΫΜOA”ΎBΓεΘ§Ν§Ϋ”AQΘ§ΙΐΒψQΉςMNΓΈOAΘ§ΫΜOC”ΎMΘ§ΫΜAB”ΎNΘ°Ω…“‘÷ΛΟςœΏΕΈMNΦΤΥψ’έΚέΘΜΉςBBΓεΒΡ¥Ι÷±ΤΫΖ÷œΏPFΘ§ΫΜOC”ΎPΘ§ΫΜAB”ΎFΘ§¥Υ ±BΓΔBΓεΙΊ”Ύ÷±œΏPFΕ‘≥ΤΘ§œΏΕΈPF“≤ «’έΚέΘ°Ζ÷±π«σ≥ωMNΓΔPFΦ¥Ω…ΫβΨωΈ ΧβΘ°

 ΤτΕΪ–ΓΧβΉς“Β±ΨœΒΝ–¥πΑΗ
ΤτΕΪ–ΓΧβΉς“Β±ΨœΒΝ–¥πΑΗ